3.8. Pullbacks and Pushouts

\section*{Pullbacks.}

Let \(f: A \to C\) and \(g: B \to C\) be two morphisms. Then we say a pullback of \(f, g\) is a commutative square on the left

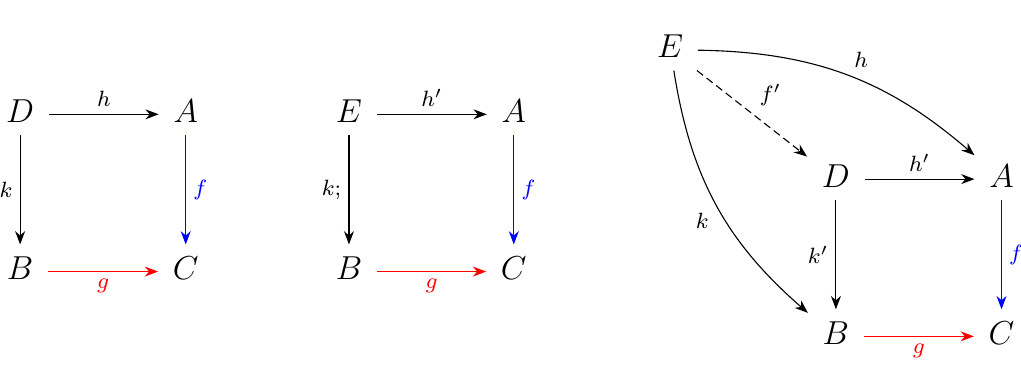such that for any commutative square in the the middle, the diagram on the right commutes, and \(f'\) is unique.

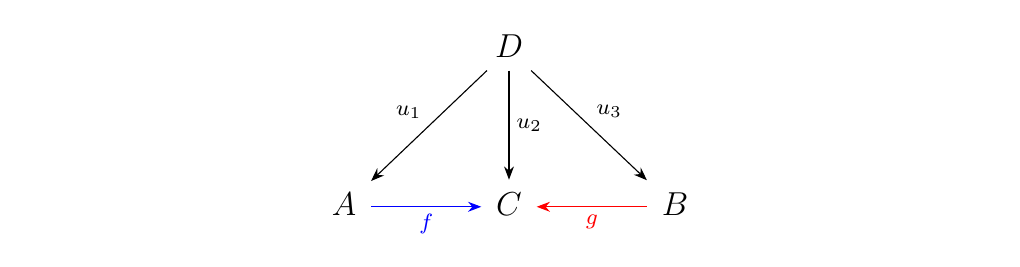
Another way we can describe this is using the language of limits, and hence show that pullbacks are simply limit objects. Let \(J\) be the category of three objects with the following shape:

The numbers 1, 2, and 3 here mean nothing; they are simply place holders for some distinct objects. So any functor \(F: J \to \cc\) simply corresponds to a triple of object and a pair of morphisms in \(\cc\):

if we have \(F(1) = A\), \(F(2) = C\) and \(F(3) = B\). Now we can equivalently describe a pullback as follows:

If \(J\) is the category with the shape $ $, and \(F: J \to \cc\) is a functor, then a pullback is a universal arrow \((D, u: \Delta(D) \to F)\) from \(\Delta\) to \(F\). First, observe that this shows that a pullback is a limit. But how are our two definitions equivalent?

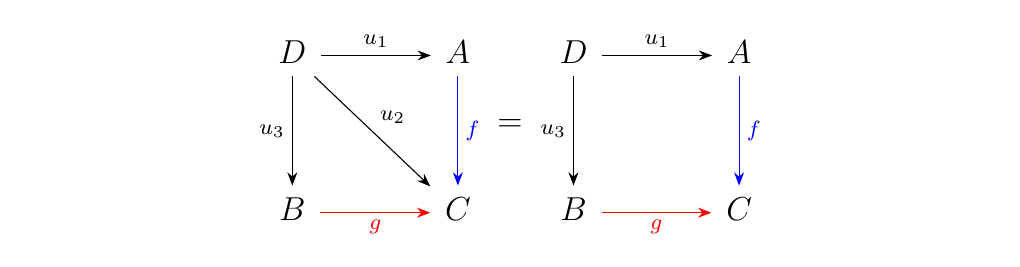
Consider the morphism \(u: \Delta(D) \to F\). This is simply a natural transformation between the two functors \(\Delta(D): J \to \cc\) and \(F: J \to \cc\). Now \(\Delta(D)(i) = D\) for all objects \(i = 1, 2, 3 \in J\). On the other hand, \(F(1) = A\), \(F(2) = C\) and \(F(3) = B\). Thus we see that \(\Delta(R) \to F\) induces a family of morphisms:

\[\begin{align*} u_1: \Delta(D)(1) \to F(1) \implies u_1: D \to A\\ u_2: \Delta(D)(2) \to F(2) \implies u_2: D \to C\\ u_3: \Delta(D)(3) \to F(3) \implies u_3: D \to B \end{align*}\]

which arrange themselves in \(\cc\) into the following diagram:

and if we "tip" this diagram over, and force the arrows \(f\) and \(g\) meeting at \(C\) into a 90 degree angle, we get the following cone:

Note that we removed the morphism \(u_2\) because it's redundant, unnecessary information; after all \(u_2 = f \circ u_1 = g \circ u_3\); which is information already captured in both the original diagram and the commutative square.

Thus, we see that whenever we have an object \(E\) and morphism \(v:\Delta(E) \to F\), we have a commutative square! In other words, whenever we have a cone over \(F\), we have a commutative square! And in even other words, whenever we have a family of morphisms \(v_i: E \to F(i)\) for \(i=1,2,3\), we have a commutative square!

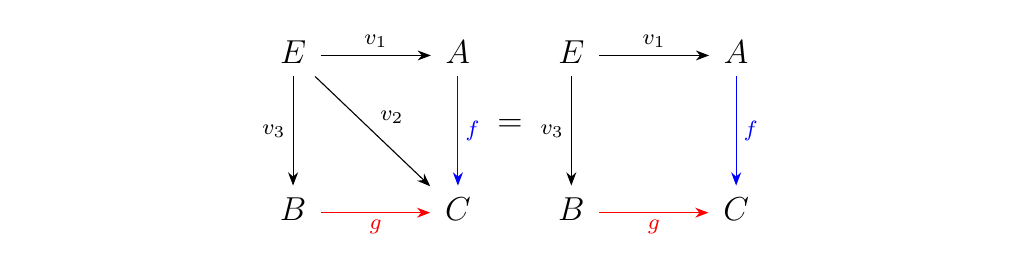
So, how do we connect the universality of \((D, u: \Delta(D) \to F)\) with the universality of the pullback? Well, since this object is universal, we know that for any other pair \((E, v: \Delta(E) \to F)\), there exists a morphism \(f': E \to D\) such that the following diagram commutes.

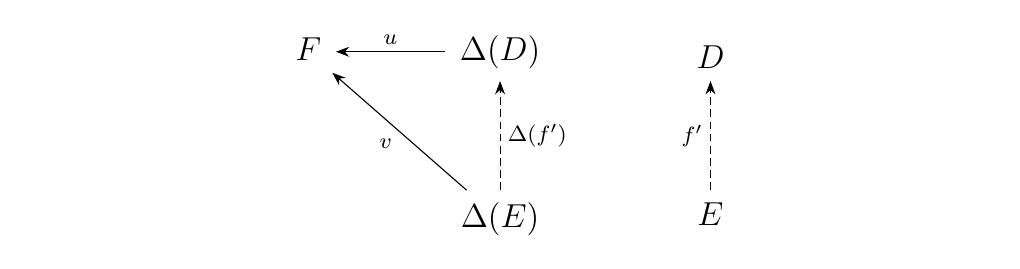The commutativity of the top left diagram gives us the relation that \(u \circ \Delta(f') = v\), which implies that \(u_1 \circ f' = v_1\) and \(u_3 \circ f' = v_3\). We then have that

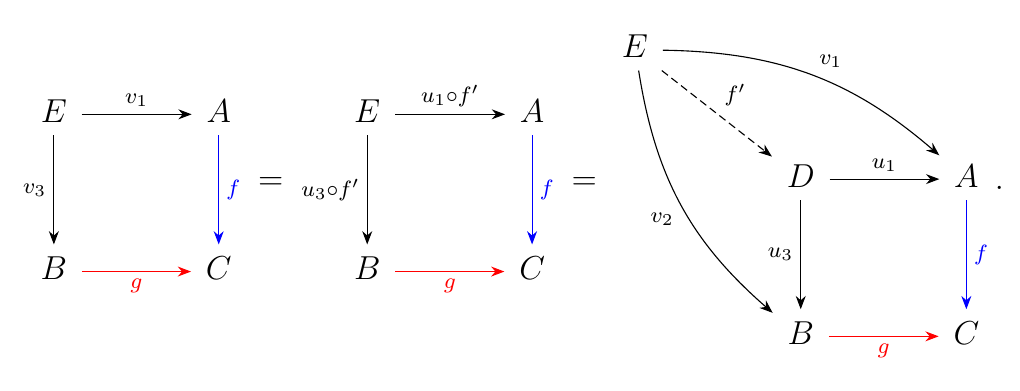which is just the pullback. Thus the pullback is in fact a limit object, and we understand just exactly how it is a limit object of the functor \(F: J \to \cc\).

Let \(\cc\) be a category, and consider a pair of morphism \(f: A \to B\), \(g:A \to C\) in \(\cc\). A pushout of \((f, g)\) is the commutative diagram on the left

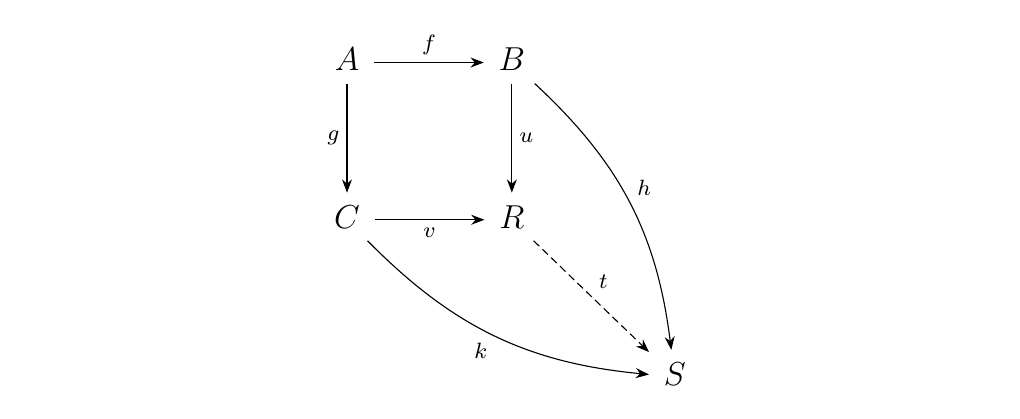
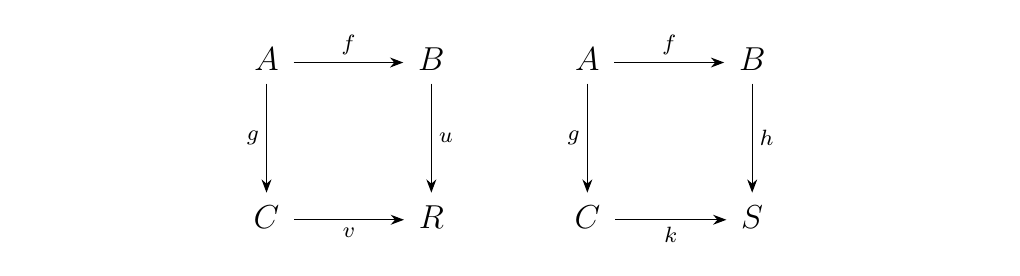such that for every commutative square as on the right, there exists a unique morphism \(t: R \to S\) such that \(t \circ u = h\) and \(t \circ v = k\). We can actually summarize this information more compactly

where the diagram is commutative. \textcolor{NavyBlue}{One way to imagine a pushout is a commutative diagram which swallows every other commutative diagram which contains the morphisms \(f, g\).}

As you might suspect, the pushout can in fact be related as the universal arrow of a functor. Consider the category 3, which contains 3 objects and two nontrivial morphisms.

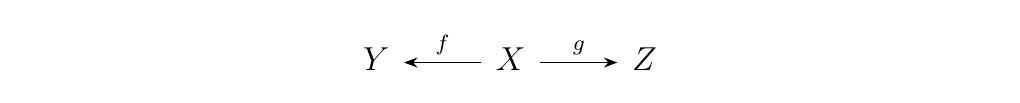Now construct the functor category \(\cc^**3**\), where

• 1. Objects are functors \(F: **3** \to \cc\), which is equivalent to pairs of morphisms \((f, g)\) where \(f: A \to B\) and \(g: A \to C\) in \(\cc\)
• 2. Morphisms are natural transformations, which in this case simply reduce to a triple of morphisms \((h, l, k)\) where

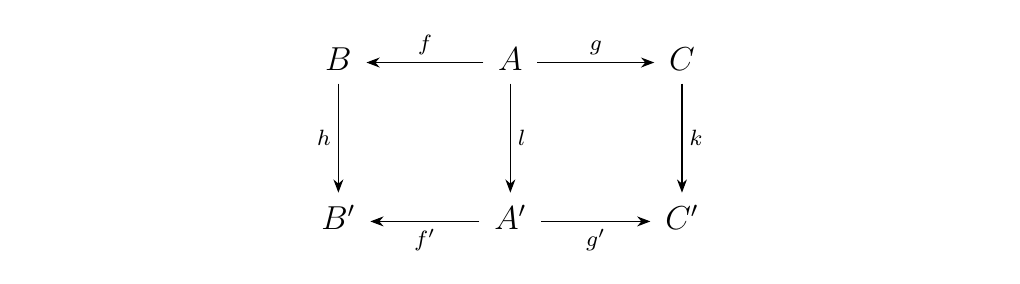
Now construct the functor \(\Delta: \cc \to \cc^**3**\) where \(C \longmapsto (1_C, 1_C)\) where \(1_C: C \to C\) is the identity morphism. Suppose there exists a natural transformation \(\eta_S: (f, g) \to \Delta(S)\), which we can represent as follows:

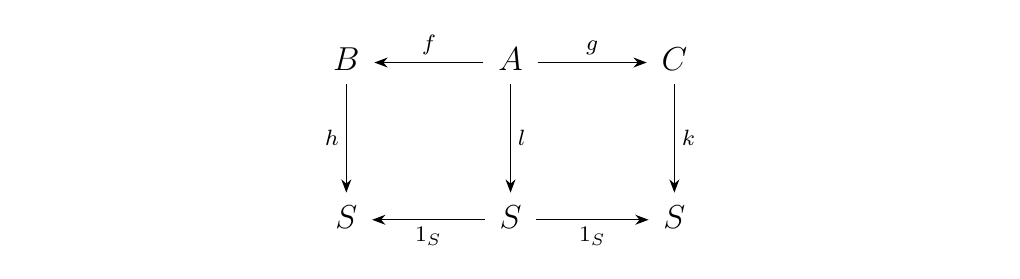If we have a pushout associated with the object \(R\) in \(\cc\), the existence of these commutative squares implies the existence of a morphism \(t: R \to S\), so that we have

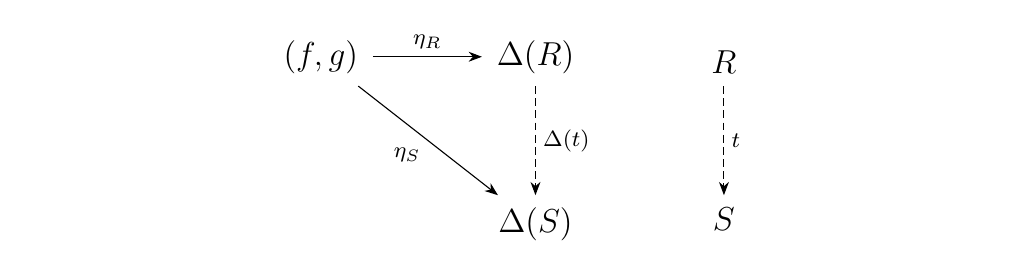Hence we see that a pushout is a universal arrow from \((f, g)\) to \(\Delta\).

\chapterimage{chapter4_pic/chapt4head.pdf}