2.4. Isomorphism Theorems.
With the concept of a quotient ring defined, we can formulate analagous Isomorphism Theorems as we had in group theory. As we move forward, recall that the main ingredients of the isomorphism theorems in group theory were normal subgroups and quotient groups. For our ring isomorphism theorems, the "normal groups" will be ideals while the "quotient groups" will be the quotient rings.
The reasons for having such analogous theorems available to us for ring theory is that \textcolor{Red}{groups are a special case of rings. The only thing that makes a group different from a ring is that we've just added a few extra axioms.} But it turns out that, even after adding these extra axioms, the Isomorphism Theorems still hold.
If you go on in algebra you'll see the Isomorphism Theorems again, proved for algebraic objects called modules. In fact, the Isomorphism Theorems were first proved by Emmy Noether in terms of modules; not groups, or rings, but the theorems hold for groups and rings since groups and rings are special cases of modules.
[(First Isomorphism Theorem.)]If \(R\) and \(S\) are rings, and \(\phi: R \to S\) is a homomorphism, then
The proof of this is analogous to the proof in group theory. We construct a homomorphism \(\phi:G/\ker(f) \to \im(f)\) by defining
Observe that for any nonzero \(s \in \im(f)\), there exists a \(r \in R\) such that \(f(r) = k\). Since \(s\) is nonzero, \(r \not\in \ker(f)\). However, observe that \(f(r + \ker(f)) = k\). Therefore \(\phi\) is surjective.
Now observe that \(\phi\) is one to one. Suppose that
for some elements \(r + \ker(f), r' + \ker(f) \in R/\ker(f)\). Then \(f(r) = f(r')\). But this implies that \(f(r) - f(r') = 0\) or that \(f(r - r') = 0 \implies r-r' \in \ker(f)\). Therefore \(r - r' = s\) for some \(s \in \ker(f)\) so that
Thus we have that \(r + \ker(f) = r' + \ker(f)\), proving that \(\phi\) is injective. Altogether we have constructed an isomorphism from \(R./\ker(f)\) to \(\im(f)\), which proves the theorem.
As an application of this, we can revisit one of the examples we computed. Earlier we found that for a homomorphism \(\phi: \RR[x] \to \mathbb{C}\) defined as
that \(\im(f) = \mathbb{C}\) and \(\ker(f) = \{p(x) \in \RR[x] \mid (x^2 + 1)\Big|p(x) \}\). Now that we can equivalently dtescribe the kernal as \(K = \{p(x) \in \RR[x] \mid p(x) = q(x)(x^2 + 1) \text{ for some } q(x) \in \RR[x]\}\). Therefore, by the First Isomorphism Theorem,
That is, the set of complex numbers is isomorphic to \(\RR[x]/K\). Well, what is this set? This set is all the elements of the form
where \(q(x) \in \RR[x]\) is an element which does not have \(x^2 + 1\) as a factor. Thus, the complex numbers are isomorphic to the equivalence class of polynomials which are not divisble by \(x^2 + 1\).
[(Second Isomorphism Theorem.)] Let \(R\) be a ring, \(I\) an ideal of \(R\), and \(S\) a subring of \(R\). Then
- 1. \(S + I\) is a subring of \(R\)
- 2. \(I\) is an ideal of \(S + I\)
- 3. \(S \cap I\) is an ideal of \(S\)
- 4. \((S + I)/I \cong S/(S \cap I)\).
\begin{minipage}{0.25 \textwidth} \begin{figure}[H]
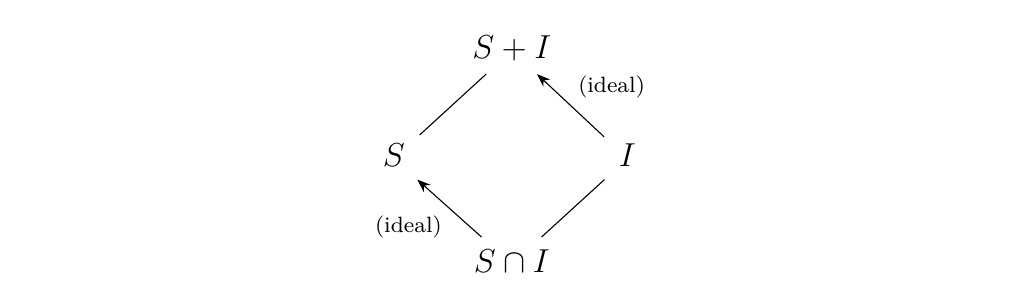
\end{figure} \end{minipage} \hfill \begin{minipage}{0.7\textwidth} The diagram on the left is analogous to the one used in the second isomorphism theorem for groups. Hence, this is again known as the diamond theorem.
Although it is important to have this diagram in mind, it is also important to remmeber that \((S + I)/I \cong S/(S\cap I)\) (given the appropriate hypotheses). \end{minipage}
- 1. To prove the first statement we first make the following connection. From the Second Isomorphism Theorem for groups, we know that \(S + I\) is an abelian group. We just need to show it is closed under multiplication. Thus let \((s + i), (s' + i') \in S + I\). Then
Therefore, we see that \((s + i)(s' + i') \in I\), so that \(S + I\) is closed under multiplication. Therefore it is a subring of \(R\). * 2. Let \(s + i \in S + I\), and let \(j \in I\). Then observe that
However, since \(I\) is an ideal, \(sj, js \in I\), and clearly \(ij, ji \in I\). Therefore, \((s + i)I \subset I\) and \(I(s + j) \subset I\) for any \((s + j) \in S + I\), which shows that \(I\) is an ideal of this set. * 3. From our study of groups, we know that \(S \cap I\) is an abelain group. We just need to check that it is closed under multiplication. Thus for any \(i \in S \cap I\) and \(s \in S\), we see that \(is \in I\) since \(I\) is an ideal.
But \(i \in S \cap I \implies i \in S\). Therfore \(is\) is also a product of two elements in \(S\).
Since \(is \in I\) and \(is \in S\), we see that \(is \in S \cap I\), proving that it is an ideal of \(S\). * 4. Consider the projection map \(\pi: R \to R/I\) restircted to \(S\), which we'll define as \(\pi|_S : S \to R/I\). (What we mean by "restricted" is that, we let \(\pi\) do its job, but we only let it act on elements in \(S \subset R\).)
Note that \(\ker(\pi|_S) = S \cap I\), while \(\im(\pi|_S) = (S + I)/I\) (namely, all the elements of the form \(s + I\) where \(s \not\in I\).) Thus by the First Isomorphism Theorem, we have that
as desired.
[(Third Isomorphism Theorem)] Let \(R\) be a ring and \(I\) and \(J\) ideals of \(R\) such that \(I \subset J\). Then
- 1. \(J/I\) is an ideal of \(R/J\)
- 2. \(R/J \cong (R/I)/(J/I)\).
For this theorem, we offer a two-in-one proof. Construct the ring homomorphism \(\phi:R/I \to R/J\) as follows:
We first demonstrate that this is well-defined. Suppose \(r + I = r' + I\); that is, there exists a \(i \in I\) such that \(r - r' = i\). Then observe that
Thus this homomorphism is well defined. Now observe that
Now the first result comes by recalling that the kernal is an ideal of the domain ring; that is, \(J/I\) is an ideal of \(R/J\). The second result comes from realizing that \(\im(f) = R/J\), and by applying the First Isomorphism Theorem to that
[(Fourth Isomorphism Theorem.)] Let \(R\) be a ring, \(S\) a subring of \(R\) and \(I\) an ideal of \(R\). Then every subring of \(R/I\) is of the form \(S/I\) where \(I \subset S \subset R\). Moreover, ideals \(J\) of \(R\) containing \(I\) correspond to ideals of \(R/I\).