7.2. Monoidal Functors
Let \((\cc, \otimes, I)\) and \((\dd, \odot, J)\) be monoidal categories. A (lax) monoidal functor is a functor \(F: \cc \to \dd\) equipped with the following data.
- For each pair \(A\), \(B\) in \(\cc\), we have a natural morphism
such that for any third object \(C\), the diagram below commutes. (Note that we suppress the subscripts for clarity.)
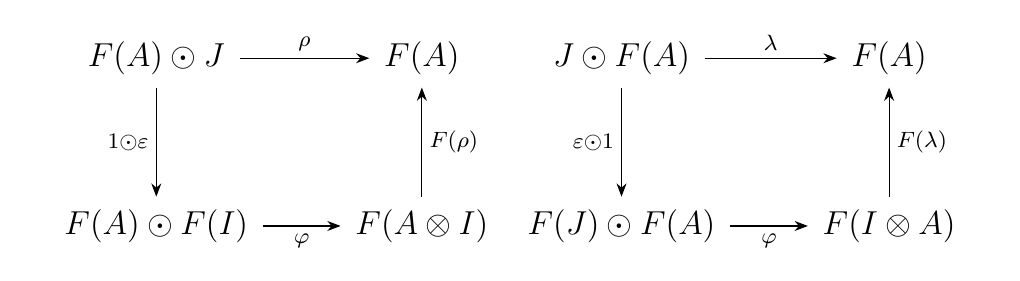
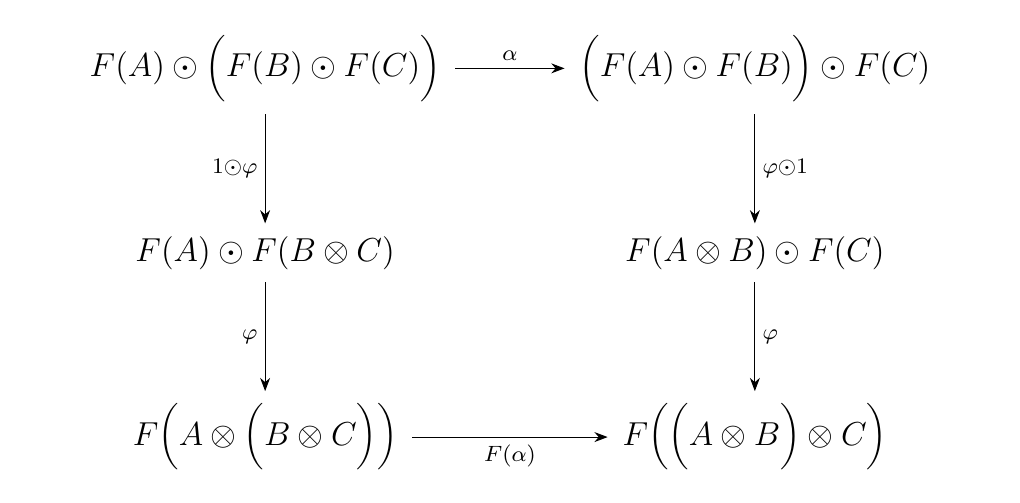 * There exists a unique morphism \(\epsilon: J \to F(I)\) such that, for any object \(A\) of \(\cc\),
the diagrams below commute. (Again,
we suppress the subscripts for clarity.)
* There exists a unique morphism \(\epsilon: J \to F(I)\) such that, for any object \(A\) of \(\cc\),
the diagrams below commute. (Again,
we suppress the subscripts for clarity.)
We say the \(F\) is strong if \(\phi\) and \(\epsilon\) are isomorphisms and strict if \(\phi\) and \(\epsilon\) are identities.
We also define a monoidal natural transformation between two monoidal functors \(\eta: F \to G\) to be a natural transformation between the functors such that, for every \(A, B\), the diagram below commutes.
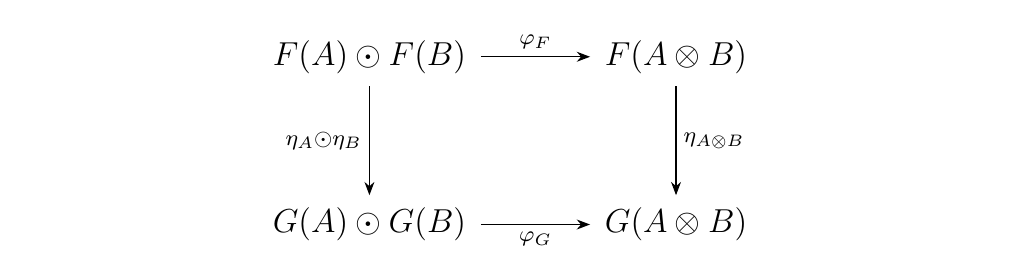
Consider the power set functor \(\mathcal{P}: **Set** \to **Set**\) which associates each set \(X\) with its power set \(\pp(X)\). We may ask if this yields a monoidal functor
in any sense of lax, strong, or strict. It turns out that we may define a lax monoidal functor, but not a strong or strict.
Towards defining a lax monoidal functor, let \(A, B\) two sets. Define \(\phi_{A,B}: \pp(A)\times\pp(B) \to \pp(A \times B)\) to be a function where if \(U, V\) are subsets of \(A, B\) respectively, then
In addition, we define the function \(\epsilon: \{\bullet\} \to P(\{\bullet\})\) where
Observe that with this data we have that for any sets \(A,B,C\), the diagram below commutes
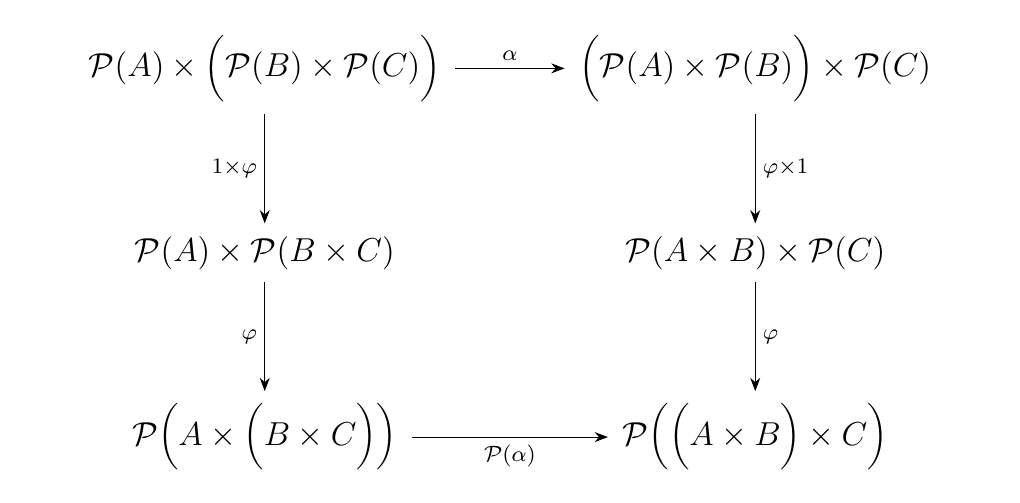 and that for any set \(A\) the diagrams below commute.
and that for any set \(A\) the diagrams below commute.
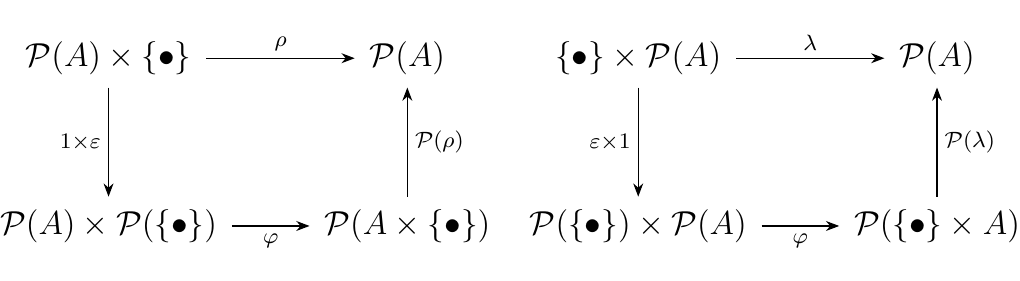 Note that our choice that \(\epsilon(\bullet) = \{\bullet\}\) was necessary in
order for the above two diagrams to commute.
Note that our choice that \(\epsilon(\bullet) = \{\bullet\}\) was necessary in
order for the above two diagrams to commute.
We now show that this cannot be a strong or strict monoidal functor. To see this, let \(A, B\) be two sets. If \(|X|\) denotes the cardinality of a set \(X\), then observe that
while
We see that in general these two sets are not of the same cardinality, and therefore one cannot establish an isomorphism between these two sets for all \(A, B\), which we would need to do to at least construct a strong monoidal functor. Hence, we cannot regard this functor as strong or strict monoidal.
The category of pointed topological spaces \(**Top**^*\) is the category where
- Objects. Pairs \((X, x_0)\) with \(X\) a topological space and \(x_0 \in X\)
- Morphisms. A morphism \(f:(X, x_0) \to (Y, y_0)\) is given by a continuous function \(f: X \to Y\) such that \(f(x_0) = y_0\).
This category is what allows us to characterize the fundamental group of a topological space as a functor
which sends a pointed space \((X, x_0)\) to its fundamental group \(\pi_1(X, x_0)\) with \(x_0\) as the selected basepoint. We demonstrate that this can be regarded as a monoidal functor
where \(\{e\}\) is the trivial group. The reader may be wondering how we are putting a cartesian product structure on the \(**Top**^*\), so we explain: For two topological spaces \(X, Y\), we define
where \(X \times Y\) is given the product topology. The identity object \((\{\bullet\}, \bullet)\) is the trivial topological space with basepoint \(\bullet\).
For any two pointed topological spaces \((X, x_0), (Y, y_0)\), define the function \(\phi_{X,Y}: \pi_1(X, x_0) \times \pi_1(Y, y_0) \to \pi(X \times Y, (x_0, y_0))\) where for two loops \(\beta, \gamma\) based as \(x_0, y_0\) respectively, then
which is in fact a loop in \(X \times Y\) based at \((x_0, y_0)\). The above function is bijective; an inverse can be constructed by sending a loop \(\delta\) in \(X \times Y\) based at \((x_0, y_0)\) to the tuple \((p\circ \delta, q \circ \delta)\) where
are the continuous projection maps. It is not difficult to see that this preserves group products, so that \(\phi_{X, Y}\) establishes the isomorphism
a fact usually proved in a topological course. In addition, this isomorphism to be natural: for two pointed topological spaces \((X, x_0)\) and \((Y, y_0)\), and for a pair of base-point preserving continuous functions \(f: (X, x_0) \to (W, w_0)\) and \(g: (Y, y_0) \to (Z, z_0)\), the following diagram commutes.
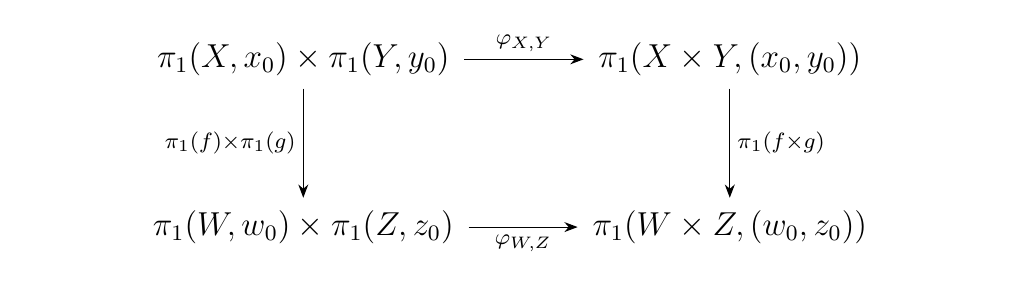 Thus \(\phi_{X,Y}\) is our desired natural isomorphism.
Thus \(\phi_{X,Y}\) is our desired natural isomorphism.
Next, define \(\epsilon: \{e\} \to \pi_1(\{\bullet\}, \bullet)\) to be the group homomorphism that takes \(e\) to the trivial loop at \(\bullet\). As in the previous example, we are actually forced to define \(\epsilon\) in this way since \(\{e\}\) is initial in Grp.
With this data, one can easily check that the necessary diagrams are commutative, so that the fundamental group functor \(\pi_1\) is strong monoidal.
Recall that a Lie algebra is a vector space \(\mathfrak{g}\) over a field \(k\) with a bilinear function \([-,-]: \mathfrak{g} \times \mathfrak{g} \to \mathfrak{g}\) such that
- Antisymmetry. For all \(x, y \in \mathfrak{g}\), \([x, y] = -[y, x]\)
- Jacobi Identity. For all \(x, y, z \in \mathfrak{g}\) we have that
For every Lie algebra \(\mathfrak{g}\), we may create the universal enveloping algebra \(U(\mathfrak{g})\). This is the algebra constructed as follows: If \(T(\mathfrak{g})\) is the tensor algebra of \(\mathfrak{g}\), i.e.,
and \(I(\mathfrak{g})\) is the ideal generated by elements of the form \(x\otimes y - y \otimes x - [x,y]\), then
By Corollary V.2.2(b) of \cite{quantumgroups}, this construction is actually a functor
Both categories can be regarded monoidal: \((**LieAlg**, \oplus, \{\bullet\})\) is the monoidal category where we apply the cartesian product between Lie algebras, and \((k**-Alg**, \otimes, k)\) is the monoidal category where we apply tensor products between \(k\)-algebras over the field \(k\). The associators and unitors are the same that we have encountered in previous examples of monoidal categories with cartesian and tensor products.
We demonstrate that the universal enveloping algebra functor is strong monoidal:
- By Corollary V.2.3 of \cite{quantumgroups}, we have that if \(\mathfrak{g_1}\) and \(\mathfrak{g_2}\) are two Lie algebras then \(U(\mathfrak{g}_1 \oplus \mathfrak{g}_2) \cong U(\mathfrak{g}_1) \otimes U(\mathfrak{g}_2)\). One can use Corollary V.2.3(a) to show that this isomorphism is natural in both \(\mathfrak{g}_1\) and \(\mathfrak{g}_2\). We let this morphism be our required isomorphism
$$
\phi_{\mathfrak{g}_1, \mathfrak{g}_2}: U(\mathfrak{g}_1\oplus \mathfrak{g}_2)
\to U(\mathfrak{g}_1)\otimes U(\mathfrak{g}_2).
$$
* Note that \(U(\{\bullet\}) = k\). Therefore, we let
\(\epsilon: k \to k\) be the identity.
As the associators and unitors are simple for monoidal categories with cartesian and tensor products, it is not difficult to show that the required diagrams commute. In this case, what is more difficult is obtaining naturality in \(\phi\), although this is taken care of (in a long proof) in Kassel's text.