5.4. Preservation of Limits
Let \(F: J \to C\) be a diagram and suppose \(G: \cc \to \dd\) is a functor. If for every limit \(\Lim F\) exists in \(\cc\) with morphisms \(u_i: C \to F_i\), we say \(G\) preserves limits if \(G(\Lim F)\) is a limit with morphisms \(G(u_i): G(C) \to G(F_i)\). Moreover, we call such a functor a continuous functor.
As an immediate consequence of the definition, it should be noted that a composition of continuous functors is continuous.
Below we see a visual definition of a continuous functor.
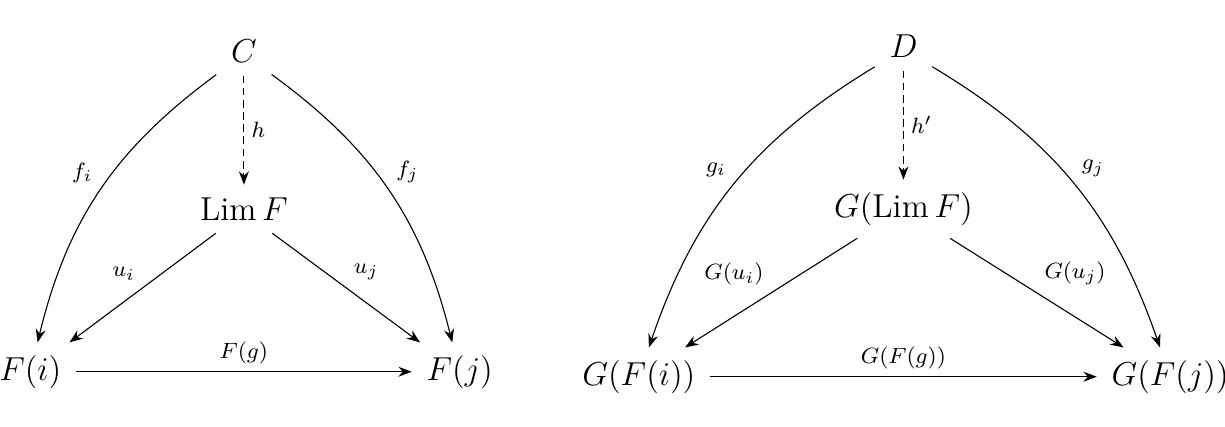 There's one particular and important functor which is always continuous
in any category.
There's one particular and important functor which is always continuous
in any category.
Let \(\cc\) be a small category. Then for each \(C \in \cc\), the functor
preserves limits. (Dually, the functor \(\hom_{\cc}(-, C) = \hom_{\cc}(C, -): \cc\op \to **Set**\) takes colimits to limits.)
Let \(F: J \to \mathcal{C}\) be a diagram with a limiting object
\(\text{Lim } F\) equipped with the morphisms \(\sigma_i: \text{Lim } F \to F_i\).
Then applying the \(\text{Hom}_{\mathcal{C}}(C, -)\) functor to \(\text{Lim } F\) and to
each \(u_i\), we realize it forms a cone in \(**Set**\).
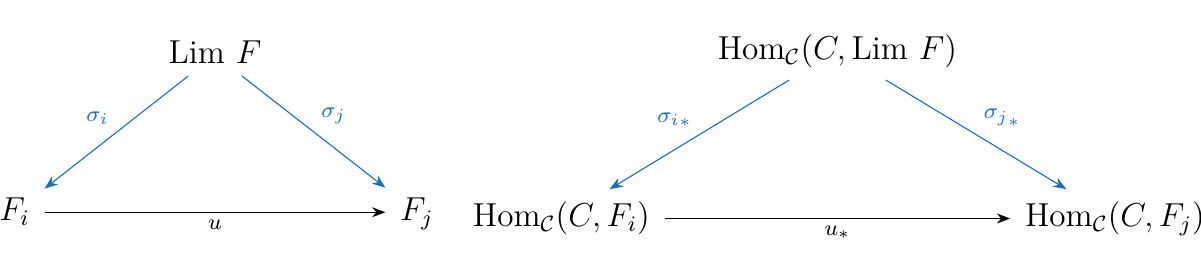 Now we show that \(\text{Hom}_{\mathcal{C}}(C, \text{Lim } F)\), equipped with the morphisms
\(\sigma_{i*}\), is a universal cone; that is, it is a limit.
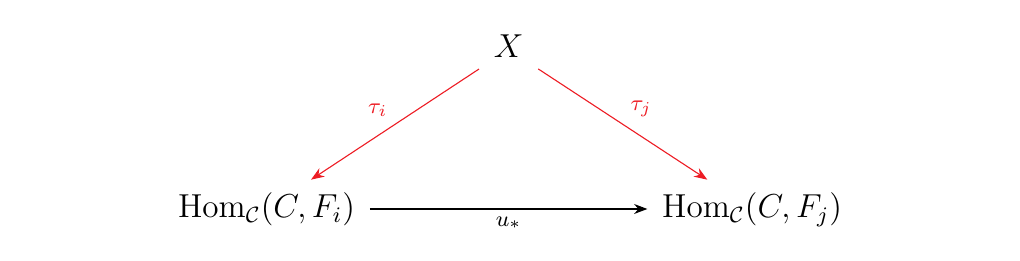
Suppose that \(X\) is a set which forms a cone with the
morphisms \(\tau_i: X \to \text{Hom}_{\mathcal{C}}(C, F_i)\).
Now we show that \(\text{Hom}_{\mathcal{C}}(C, \text{Lim } F)\), equipped with the morphisms
\(\sigma_{i*}\), is a universal cone; that is, it is a limit.
Suppose that \(X\) is a set which forms a cone with the
morphisms \(\tau_i: X \to \text{Hom}_{\mathcal{C}}(C, F_i)\).
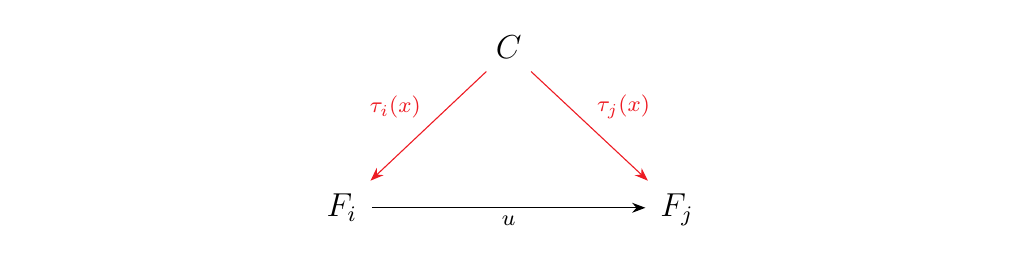
Then for each \(x \in X\), we see that \(\tau_i(x) : C \to F_i\). The diagram above tells us that \(u \circ \tau_i(x) = \tau_j(x)\) for each \(x\). Hence each \(x \in X\) induces a cone with apex \(C\) with morphisms \(\tau_i(x): C \to F_i\).
 However, \(\text{Lim } F\) is the limit of \(F: J \to \mathcal{C}\). Therefore, there
exists a unique arrow \(h_x: C \to \text{Lim } F\) such that
\(h_x \circ \sigma_i = \tau_i(x)\). Now we can uniquely
define a function \(: X \to \text{Hom}_{\mathcal{C}}(C, \text{Lim } F)\) where
\(h(x) = h_x: C \to \text{Lim } F\), in such a way that the diagram below commutes.
However, \(\text{Lim } F\) is the limit of \(F: J \to \mathcal{C}\). Therefore, there
exists a unique arrow \(h_x: C \to \text{Lim } F\) such that
\(h_x \circ \sigma_i = \tau_i(x)\). Now we can uniquely
define a function \(: X \to \text{Hom}_{\mathcal{C}}(C, \text{Lim } F)\) where
\(h(x) = h_x: C \to \text{Lim } F\), in such a way that the diagram below commutes.
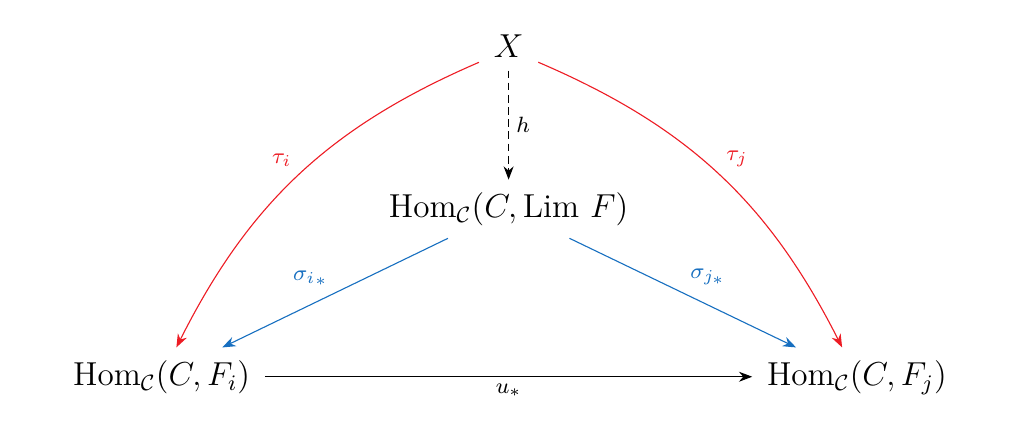 Therefore, \(\text{Hom}_{\mathcal{C}}(C, \text{Lim } F)\) is a limit in Set.
At this point, you may be wondering: What is the difference between
a functor which "creates limits" and one which preserves them?
We'll see that their definitions are different, but creating limits
is the same as preserving them
Therefore, \(\text{Hom}_{\mathcal{C}}(C, \text{Lim } F)\) is a limit in Set.
At this point, you may be wondering: What is the difference between
a functor which "creates limits" and one which preserves them?
We'll see that their definitions are different, but creating limits
is the same as preserving them
Suppose \(G: \cc \to \dd\) creates limits for \(F: J \to \cc\). If \(G \circ F: J \to \dd\) has a limit in \(\dd\), then \(G\) is continuous.
Suppose \(F: J \to \cc\) has limit \(\Lim F\) in \(\cc\) with morphisms \(v_i: \Lim F \to F_i\) for each \(i \in J\). Further, suppose \(G \circ F: J \to \dd\) has a limit \(\Lim G \circ F\) with morphisms \(u_i: \Lim G \circ F \to G\circ F_i\).
Since \(G: \cc \to \dd\) creates limits, this implies
the existence of a limiting object \(X\) with morphisms
\(\sigma_i: X \to F_i\) for \(F: J \to C\)
where \(G(X) = \Lim G\circ F\) and \(G(\sigma_i) = u_i\).
However, limiting objects are unique (by their universal properties).
As they must be isomorphic, there exists an isomorphism
\(\phi: X \to \Lim F\) for which \(v_i \circ \phi= \sigma_i\).
Thus we see that
Therefore, \(G\) preserves limits and so is continuous.
We have the following as a corollary.
Suppose \(G: \cc \to \dd\) creates limits and \(\cc\) is complete. Then \(\dd\) is complete and \(G\) preserves limits.