1.2. Motivation for Category Theory

What do groups \(G\), topological spaces \(X\) and vector spaces \(V\) have in common? We use different letters to describe them! Seriously, that is one major difference. Why? Because our brains are organizational and thrive off of associations, e.g., \(G\) with group, \(X\) with topological spaces, etc. This is great for thinking, but the mental separation of these constructions hides a bigger picture.

Let's look at what these things look like. With groups, we are often mapping between groups via group homomorphisms. For example, below we have the chain complex of abelian groups with boundary operator \(\partial_n: C_n \to C_{n-1}\), with the familiar property that \(\partial_n \circ \partial_{n-1} = 0\).

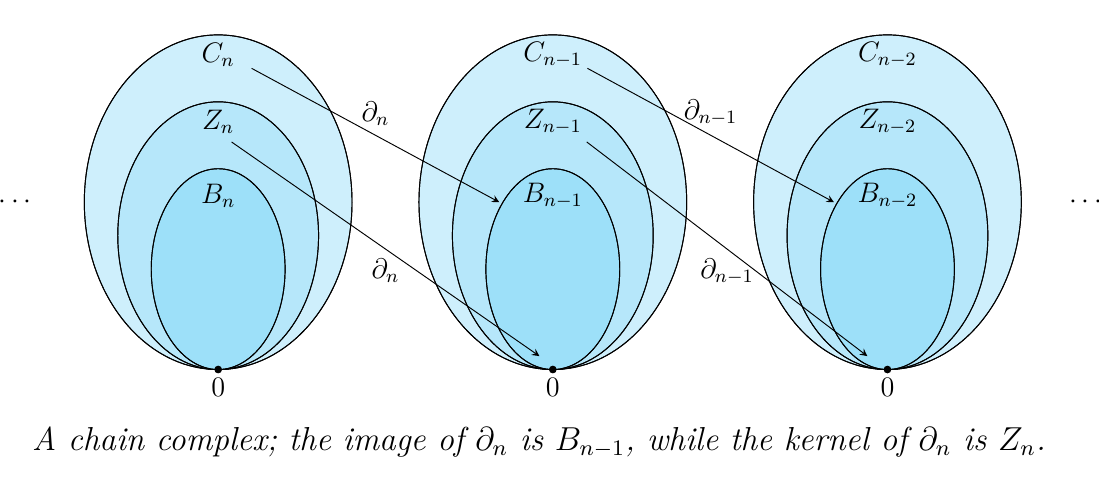
Within topology, we are often mapping topological spaces via continuous functions.

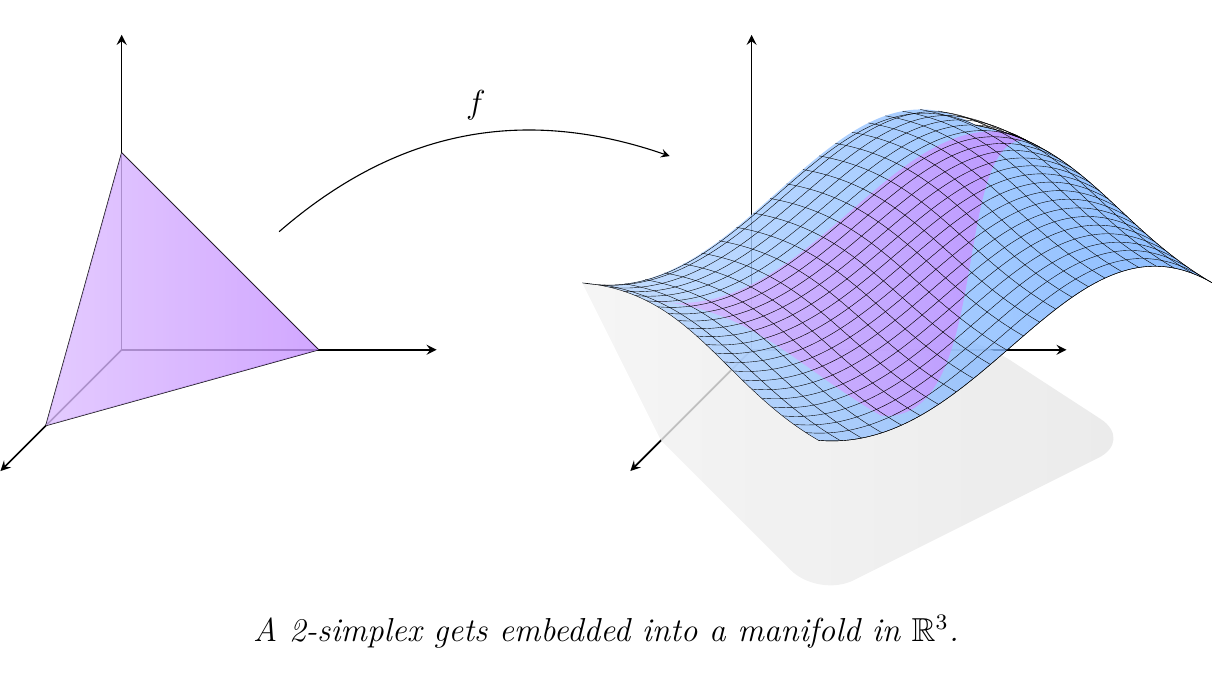
With vector spaces, we often use linear transformations to map from one to another.

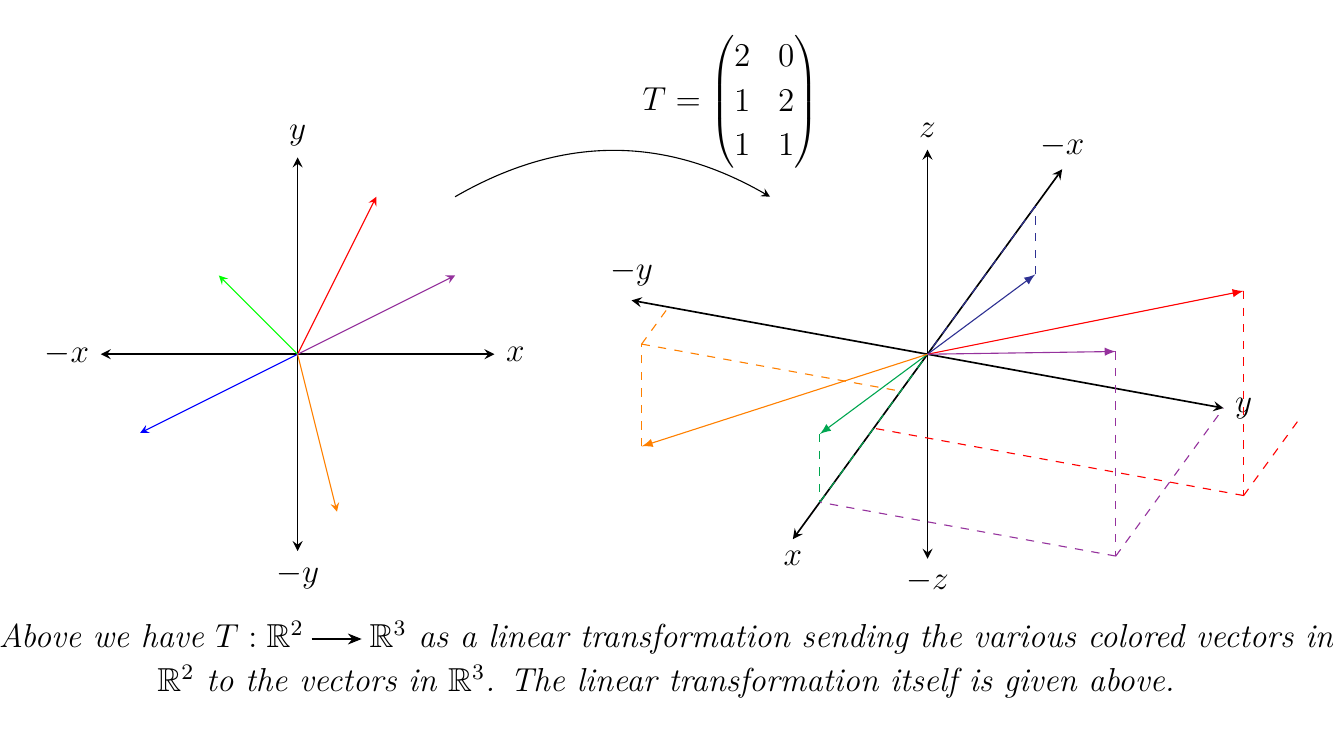At some point when we're learning different basic constructions in pure mathematics, we often realize that we're just repeating the same story over and over. The professor tells you about an object (usually a set) equipped with some axioms. The next thing you learn are "mappings" between such objects, which can abstractly be called morphisms. The characteristics of these morphism are generally the following:

• 1. There's an identity morphism.
• 2. There's a notion of composition.
• 3. Composition is associative.
• 4. Composing identities in any order with a morphism returns the same morphism.

What is it that I just described? It sounds just like a monoid! In the most basic sense, a monoid \(M = \{x_1, x_2, \dots, \}\) is a set of elements equipped with a multiplication map

\[ \cdot: M \times M \to M \qquad (x, y) \mapsto x\cdot y \]

which is associative, and with a multiplicative identity \(e\). With a monoid we see that

• 1. There's an identity \(e\).
• 2. There's a notion of multiplication.
• 3. Multiplication is associative.
• 4. Multiplying \(e\) in any order with an element \(x\) returns \(x\).

The concept of a monoid is one of the most underrated yet powerful concepts of mathematics, and for some reason it's usually ignored in algebra courses. It's an innate, fundamental human concept, a consequence of our physical reality. How many years have our ancestors been saying: "Let's stack stuff together and see what happens!" Stacking three things in two different ways is the same. Stacking nothing is an "identity". Thus what we see is that groups, topological spaces and vector spaces are all similar in that (1) we have morphisms of interest and (2) the morphisms behave like a monoid. This notion is what category theory takes care of.