2.2. Products of Categories, Functors

As one may expect, the product of categories can be easily defined.

Let $\cc$ and $\dd$ be categories. Then the product category $\cc \times \dd$ is the category where

Objects. All pairs $(C, D)$ with $C \in \ob(\cc)$ and $D \in \ob(\dd)$
Morphisms. All pairs $(f, g)$ where $f \in \hom(\cc)$ and $g \in \hom(\dd)$.

To define composition in this category, suppose we have composable morphisms in $\cc$ and $\dd$ as below.

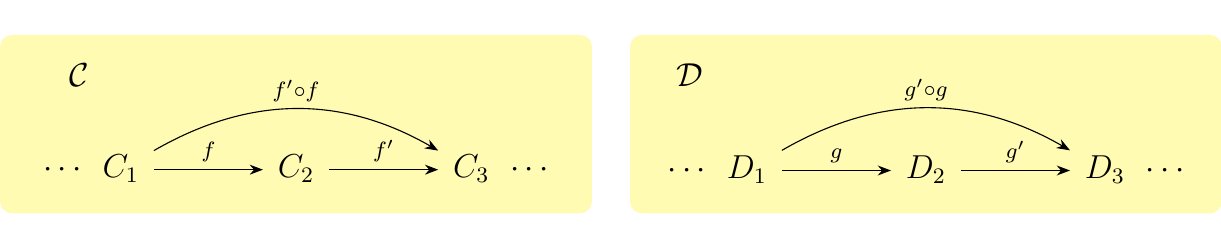Then the morphisms $(f, g)$ and $(f', g')$ in $\cc \times \dd$ are composable too, and their composition is defined as $(f', g') \circ (f , g) = ( f' \circ f, g' \circ g)$.

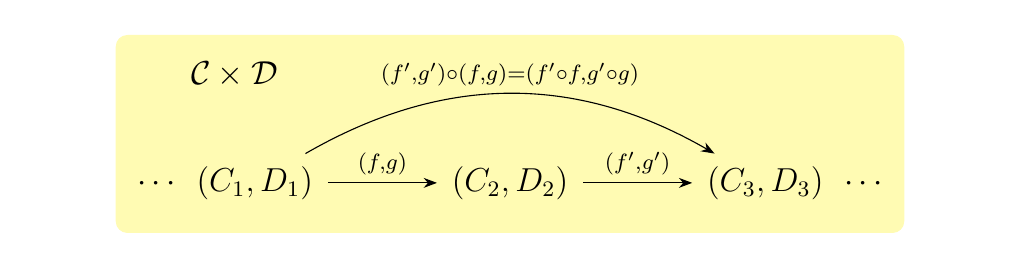
We also define the projection functors $\pi_\cc: \cc\times\dd \to \cc$ and $\pi_\dd: \cc\times\dd \to \dd$ where on objects $(C, D)$ and morphism $(f, g)$, we have that

\[\begin{align*} &\pi_\cc(C, D) = C \quad &&\pi_\dd(C, D) = D\\ &\pi_\cc(f, g) = f \quad &&\pi_\dd(f, g ) = g \end{align*}\]

These projection functors have the following property. Consider a pair of functors $F: \bb \to \cc$ and $G:\bb \to \dd$. Then $F$ and $G$ determine a unique functor $H: \bb \to \cc \times \dd$ where

\[ \pi_\cc \circ H = F \qquad \pi_\dd \circ H = G. \]

That is, we see that for any morphism $f$ in $\bb$ we have that $H(f) = ( F(f), G(f) )$. Hence the following diagram commutes

and we dash the middle arrow to represent that $H$ is induced, or defined, by this process.

We can also take the product of two different functors.

Let $F: \cc \to \cc'$ and $G: \dd \to \dd'$ be two functors. Then we define the product functor to be the functor $F \times G: \cc \times \dd \to \cc' \times \dd'$ for which

1. If $(C, D)$ is an object of $\cc\times\dd$ then $(F\times G)(C, D) = (F(C), G(D))$
2. If $(f, g)$ is a morphism of $\cc\times\dd$ then $(F \times G)(f,g) = (F(f), G(g))$

Additionally, we can compose the product of functors (of course, so long as they have the same number of factors). Thus suppose $G,F$ and $G', F'$ are composable functors. Then observe that

\[ (G \times G') \circ (F \times F') = (G \circ F) \times (G' \circ F'). \]

Note that in this formulation we have that

\[ \pi_{\cc'}\circ (F\times G) = F \circ \pi_\cc \quad \pi_{\cc'} \circ (F \times G) = G \circ \pi_{\dd} \]

Hence, we have the following commutative diagram.

Again, the dashed arrow is written to express that $F \times G$ is the functor defined by this process and makes this diagram commutative.

If $F$ is a functor such that $F: \bb \times \cc \to \dd$, that is, its domain is a product category, then $F$ is said to be a bifunctor.

An example of a bifunctor is the cartesian product $\times$, which we can apply to sets, groups, and topological spaces. In these instances we know that value of a cartesian product is always determined uniquely by the values of the individual factors, which holds more generally for bifunctors.

Let $\bb, \cc$ and $\dd$ be categories. For $B \in \bb$ and $C \in \cc$, define the functors

\[ H_C: \bb \to \dd \quad K_B: \cc \to \dd \]

such that $H_C(B) = K_B(C)$ for all $B, C$. Then there exists a functor $F:\bb \times \cc \to \dd$ where $F(B, -) = K_B$ and $F(-, C) = H_C$ for all $B, C$ if and only if for every pair of morphisms $f:B \to B'$ and $g:C\to C'$ we have that

\[ K_{B'}(g) \circ H_C(f) = H_{C'}(f) \circ K_B(g). \]

Diagrammatically, this condition is

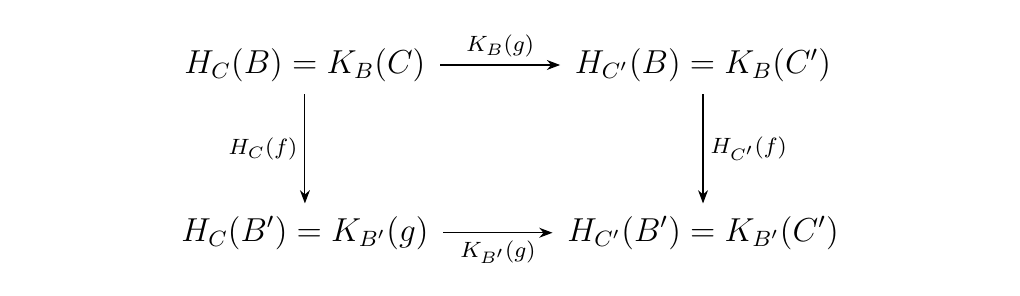
The proof is left as an exercise for the reader.

We now introduce what is probably one of the most important examples of a bifunctor. Note that for any (locally small) category $\cc$, we have for each object $A$ a functor.

\[ \hom(A, -): \cc \to **Set** \]

We also have a functor from $\cc\op$ (we at the $\op$ simply for convenience) for each $B \in \cc\op$.

\[ \hom(-, B): \cc\op \to **Set** \]

As an application of the proposition, one can see that that these two functors act as the $K_B$ and $H_C$ functors in the above proposition, and give rise to bifunctor

\[ \hom: \cc\op \times \cc \to **Set**. \]

This is because for any $h: A \to A'$ and $k: B \to B'$, the diagram,

commutes. Hence the proposition guarantees that $\hom:\cc\op\times\cc \to **Set**$ exists and is unique.

Recall that for an integer $n$ and for a ring $R$ with identity $1 \ne 0$,
we can formulate the group $\text{GL}(n, R)$, consisting of $n\times n$ matrices with entry values in $R$. As this takes in arguments, we might guess that we have a bifunctor

\[ GL(-, -): \bm{\mathbb{N}} \times **Ring** \to **Grp** \]

where $\bm{\mathbb{N}}$ is a the discrete category with elements as natural numbers. This intuition is correct: for a fixed ring $R$, we have a functor

\[ GL(-, R): \bm{\mathbb{N}} \to **Grp** \]

while for a fixed natural number $n$ we have a functor

\[ GL(n, -): **Ring** \to **Grp**. \]

Below we can visualize the activity of this functor:

Above, we start with $\zz$ since the this is the initial object of the category Ring.

Now that we understand products of categories a functors, and we have a necessary and sufficient condition for the existence of a bifunctor, we describe necessary and sufficient conditions for the existence of a natural transformation.

Suppose $F, G: \bb \times \cc \to \dd$ are bifunctors. Suppose that there exists a morphism $\eta$ which assigns objects of $\bb \times \cc$ to morphisms of $\dd$. Specifically, $\eta$ assigns objects $B \in \bb$ and $C \in \cc$ to the morphism

\[ \eta_{(B, C)} : F(B, C) \to G(B, C). \]

Then $\eta$ is said to be natural in $B$ if, for all $C \in \cc$,

\[ \eta_{(-, C)} : F(-, C) \to G(-, C) \]

is a natural transformation of functors from $\bb \to \dd$.

With the previous definition, we can now introduce the necessary condition for a natural transformation to exist between bifunctors.

Let $F, G: \bb \times \cc \to \dd$ be bifunctors. Then there exists a natural transformation $\eta: F \to G$ if and only if $\eta(B, C)$ is natural in $B$ for each $C \in C$, and natural in $C$ for each $B \in \bb$.

($\bm{\implies}$) Suppose that $\eta: F \to G$ is a natural transformation. Then every object $(B, C)$ is associated with a morphism $\eta_{(B, C)}: F(B, C) \to G(B, C)$ in $\dd$, and this gives rise to the following diagram:

Now let $C \in \cc$ and observe that

\[ \eta_{(-, C)}: F(-, C) \to G(-,c) \]

is a natural transformation for all $B$. On the other hand, for any $B \in \bb$,

\[ \eta_{(B, -)}: F(B, -) \to G(B, -) \]

is a natural transformation for all $C$. Therefore, $\eta$ is both natural in $B$ and $C$ for all objects $(B, C)$ * ($\bm{\impliedby}$) Suppose on the other hand that $\eta$ is a function which assigns objects $(B, C)$ to a morphism $F(B, C) \to G(B, C)$ in $\dd$. Furthermore, suppose that $\eta(B, C)$ is natural in $B$ for all $C \in \cc$ and natural in $C$ for all $B \in \bb$.

Consider a morphism $(f, g) : (B, C) \to (B', C')$ in $\bb \times \cc$. Then since $\eta$ is natural for all $B \in \bb$, we know that for all $C \in \cc$,

\[ \textcolor{red}{\eta}_{(-, C)} : F(-, C) \to G(-,C) \]

is a natural transformation. In addition, $\eta$ is natural for all $C \in \cc$ since for all $B \in \bb$

\[ \textcolor{blue}{\eta}_{(B, -)} : F(B, -) \to G(B, -) \]

is a natural transformation. Hence consider the natural transformation $\textcolor{red}{\eta}_{(-, C)}$ acting on $(B, C)$ and $\textcolor{blue}{\eta}_{(B', -)}$ acting on $(B', C)$. Then we get the following commutative diagrams.

Observe that the bottom row of the first diagram matches the top row of the second. Also note that $f: B \to B'$ and $g: C \to C'$, and that the diagrams imply the equations

\[\begin{align} G(f, 1_C) \circ \textcolor{red}{\eta}_{(B,C)} &= \textcolor{red}{\eta}_{(B', C)} \circ F(f, 1_C) \\ G(1_{B'}, g) \circ \textcolor{blue}{\eta}_{(B', C)} &= \textcolor{blue}{\eta}_{(B', C')} \circ F(1_{B'}, g). \end{align}\]

Now suppose we compose equation (\ref{eq1_prop_2_2}) with $G(1_{B'}, g)$ on the left. Then we get that

\[\begin{align*} G(1_{B'}, g)\circ G(f, 1_C) \circ \textcolor{red}{\eta}_{(B, C)} &= \overbrace{G(1_{B'}, g) \circ \textcolor{red}{\eta}_{(B', C)}}^{\text{replace via equation (2)}} \circ F(f, 1_C)\\ &= \textcolor{blue}{\eta}_{(B', C')} \circ F(1_{B'}, g) \circ F(f, 1_C)\\ &= \textcolor{blue}{\eta}_{(B',C')} \circ F(1_{B'}\circ f, g \circ 1_C)\\ &=\textcolor{blue}{\eta}_{(B',C')} \circ F(f, g). \end{align*}\]

where in the second step we applied equation (\ref{eq2_prop_2_2}), and in the third step we composed the morphisms. Also note that we can simplify the left-hand side since

$$ G(1_{B'}, g)\circ G(f, 1_C) = G(1_{B'}\circ f, g \circ 1_C) = G(f, g). $$ Therefore, we have that

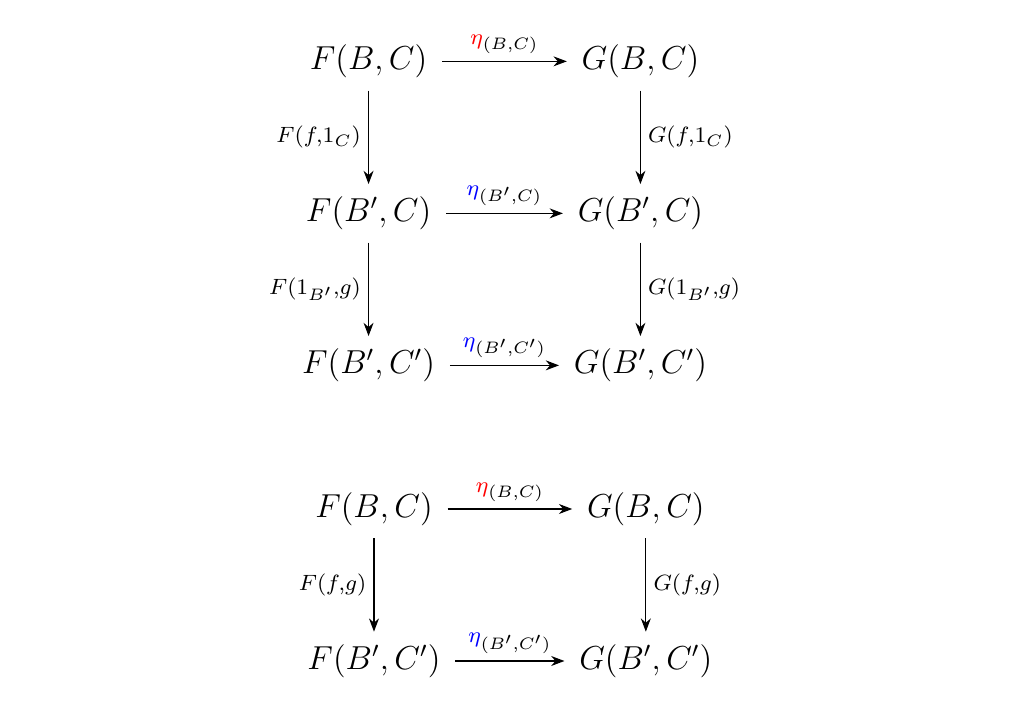
\[ G(f, g) \circ \textcolor{red}{\eta}_{(B, C)} = \textcolor{blue}{\eta}_{(B', C')} \circ F(f, g) \]

which implies that $eta$ itself is a natural transformation. Specifically, it implies the following diagram.

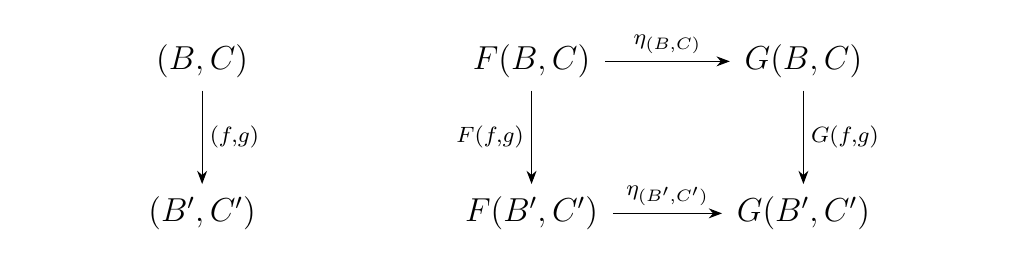
Note: A way to succinctly prove the reverse implication of the previous proof is as follows. Since we know the diagrams on the left are commutative, just "\textcolor{Green}{stack}" them on top of each other to achieve the diagram in the upper right corner, and then "\textcolor{Orange}{squish}" this diagram down to obtain the third diagram in the bottom right.

\begin{minipage}{0.3\textwidth}

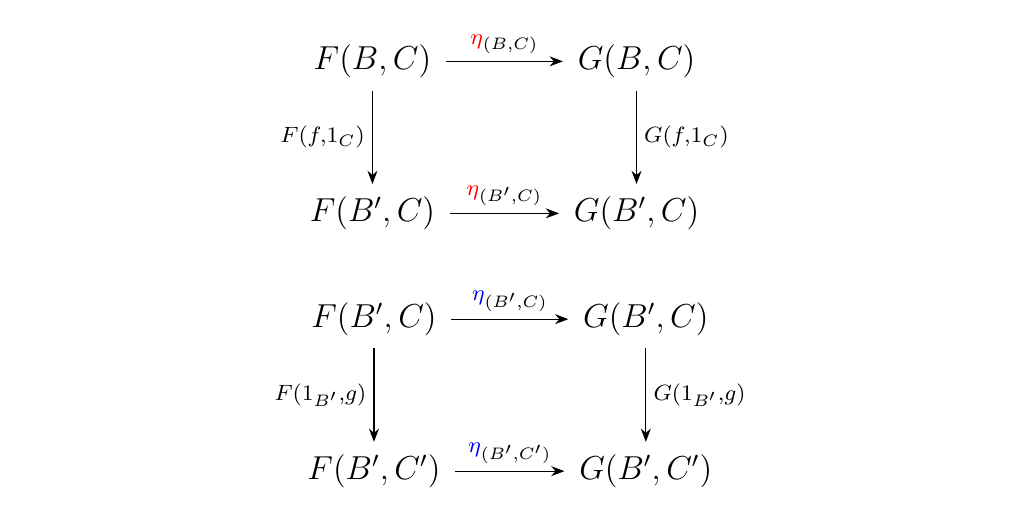\end{minipage}
\hspace{1cm} \begin{minipage}{0.1\textwidth}

\end{minipage} \hfill \begin{minipage}{0.5\textwidth}

\end{minipage} \vspace{1cm}

This is essentially what we did in the proof, although this is more crude visualization of what happened, and we were more formal throughout the process.

{\large Exercises \vspace{0.5cm}}

*1.* Let $\cc$ and $\dd$ be categories. Prove that $(\cc \times \dd)\op \cong \cc\op\times\dd\op$.