5.3. Limits from Products, Equalizers, and Pullbacks.

In our construction of limits for Sets, we basically forced the existence of a cone, because we could. This is usually the general strategy when it comes to calculating the limit of a diagram in a given category; one uses available, useful constructions which are already present inside of a category. For example; in Set, we used the fact that it is cartesian closed to formulate infinite products.

Since the general strategy for showing Set is complete can be extended to other categories, one may wonder "well, why? And when will I no longer be able to apply this strategy?" The theorem below answers this question.

Let \(\cc\) be a category and \(J\) a small category. Suppose \(\cc\) has equalizers for every pair of morphisms in \(\cc\), and all products indexed by objects of \(J\) and morphisms of \(J\). Then every functor \(F: J \to \cc\) has a limit in \(\cc\).

\textcolor{purple}{What do we mean by all products "indexed by objects of \(J\) and morphisms of \(J\)"?} What we want to do is be able to create products of the form

\[ \prod_{j \in J}F_j \qquad\qquad \prod_{u:i \to k} F_\text{\text{cod}(u)} = \prod_{u:j \to k}F_k. \]

and know that they're in \(\cc\). The product on the far left is indexed by objects of \(J\), while the equal
ones on the right are indexed by morphisms \(u: i \to k\) in \(J\). It's a bit weird to think of a product "indexed by morphisms," but it's
exactly what it sounds like: we index over all the morphisms, and take the product of the domain or codomain (in the above, we did codomain).

\textcolor{purple}{Why do we need this weird concept?} To answer this, let's go over the construction of limits in Set in a bit different way.

When we had a diagram \(F: J \to \cc\) in \(\cc\), our first guess in constructing the limit was designing the \(\displaystyle \prod_{j}F_j\) with morphisms \(\displaystyle \pi_i : \prod_{j}F_j \to F_i\). However, this doesn't actually form a cone, since for each \(u: j \to k\), we can't guarantee

\[ F(u) \circ \pi_j = \pi_k \]

That is, we can't guarantee the diagram

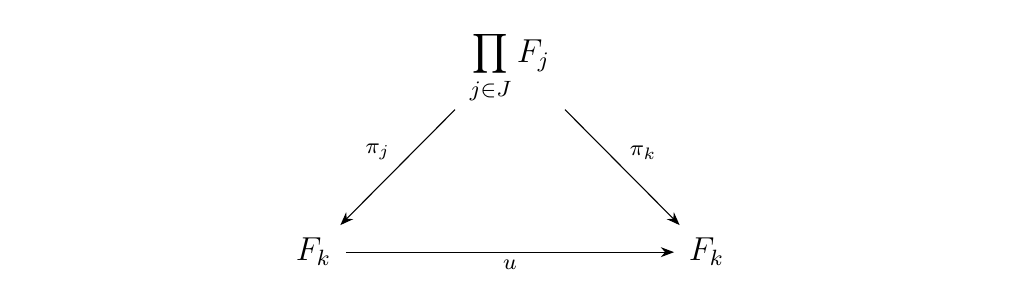will commute, which is what we need for a cone. Since we needed \(F(u) \circ \pi_j = \pi_k\), we forced it. But this forcing is simply realizing that, all \(\displaystyle x \in \prod_{j \in J}F_j\) which satisfy \(F(u) \circ \pi_j = \pi_k\), are simply members of the equalizer of \(F(u) \circ \pi_j\) and \(\pi_k\).

Consider the products \(\displaystyle \prod_{j \in J}F_j\) and \(\displaystyle \prod_{u: i \to k}F_k\) where in the last product we index over all morphisms in \(J\). With both products, consider the projection morphisms

\[\begin{align*} &\pi'_j: \prod_{u:i \to k}F_k \to F_j\\ &\pi_j: \prod_{i \in J}F_i \to F_j. \end{align*}\]

Note that because we have products, we have universal properties which we can take advantage of. That is, the following diagrams must commute for some \(f\) and \(g\).

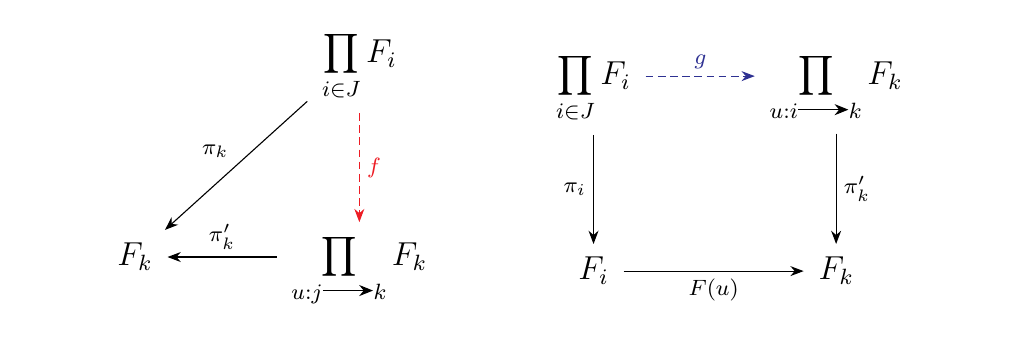Note however that we can stack these diagrams on top of each other, to obtain

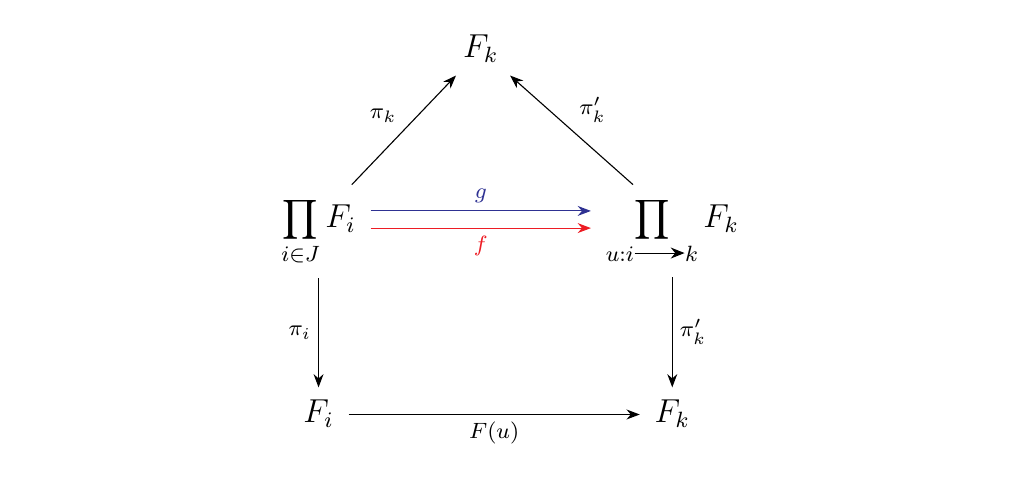Since we have equalizers for every pair of arrows, we can form the equalizer \(\displaystyle e:D \to \prod_{i \in J}F_i\) of both \(f\) and \(g\) for some object \(D\).

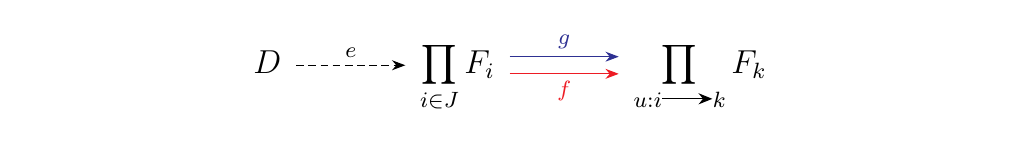
Now that we have a morphism \(\displaystyle e: D \to \prod_{i \in J}F_i\),
we can compose this with projections \(\displaystyle \prod_{i \in J}F_i \to F_i\) to produce a family of morphisms \(\pi_i \circ e: D \to F_i\). If we like, we can even add this to our diagram above to get the following:

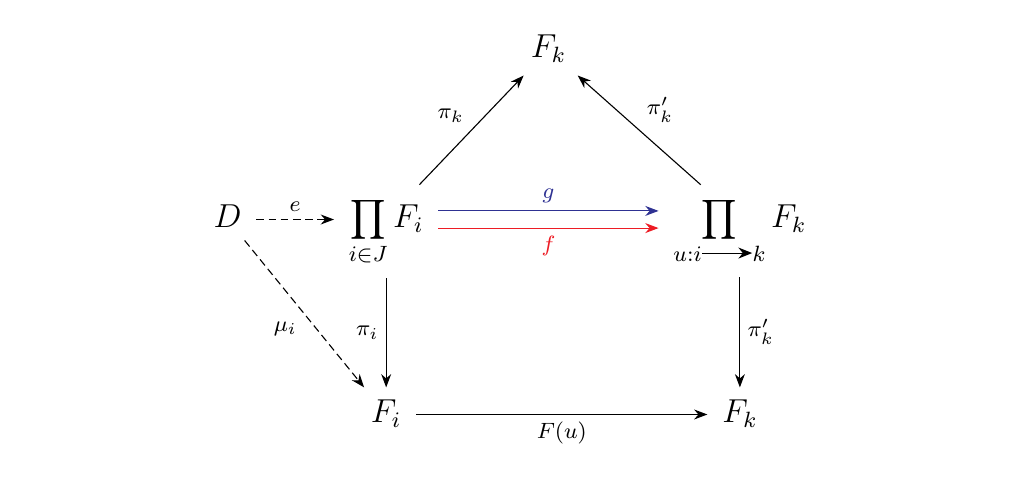(\textcolor{Red}{It looks like a boat!}) Denote \(\mu_i = \pi_i \circ e: D \to F_i\). Then what the above boat diagram tells us is that

\[ \pi'_k \circ g = \pi_k \qquad F(u)\circ \pi_i = \pi'_k \circ f. \]

Composing both equations with \(e\), we get

\[ \pi'_k \circ g \circ e = \pi_k \circ e \qquad F(u)\circ \pi_i \circ e= \pi'_k \circ f\circ e. \]

but since \(g \circ e = f \circ e\), what this really tells us is that

\[ F(u) \circ \pi_i \circ e = \pi_k \circ e \implies F(u) \circ \mu_i = \mu_k. \]

for every \(u: i \to k\) in \(J\). Therefore, we see that we have that

commutes, so that \(D\) equipped with the morphisms \(\mu_i: D \to F_i\) forms a cone. We now show that this is universal, so that \(D\) is our limit. We do this by taking advantage of the universal property which equalizers posses.

Suppose \(C\) is another object which forms a cone with morphisms \(\tau_i: C \to F_i\). Then there exists a map \(\displaystyle e': C \to \prod_{i \in J}F_i\) such that \(\pi \circ e' = \tau_i\). Moreover, this implies that \(f \circ e = g \circ e\). But the universal property of the equalizer \(e\) states that for any subject object, there exists a morphism \(h: D \to C\) such that the diagram below commutes.

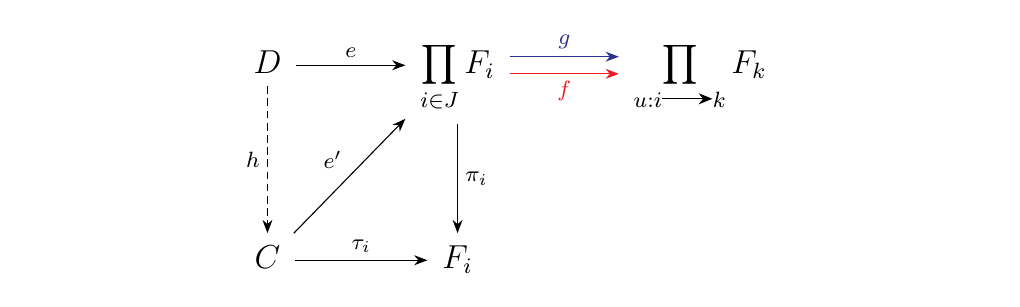Since \(h: D \to C\) is unique, this shows that \(D\) equipped with the morphisms \(\displaystyle \mu_i: D \to F_i\) forms a limit of the diagram, so that \(D = \Lim F\). We actually proved much more than what was stated in the theorem, since we literally found the explicit form the limit.

As a corollary, we have the following result which is due to the above theorem. The only difference is we strengthen our hypothesis, which makes it less general.

Let \(\cc\) be a category. If \(\cc\) has all equalizers (coequalizers) and finite products (coproducts), then \(\cc\) has all finite limits (colimits).

By Proposition \ref{prop_category_finite_products}, one can obtain finite products by simply demanding the existence of binary products and a terminal object. Hence we can restate the above corollary:

Let \(\cc\) be a category. If \(\cc\) has all equalizers (coequalizers), binary products (coproducts) and a terminal object, then \(\cc\) has all finite limits.

Not what is even more interesting is that we can construct equalizers and finite products from pullbacks.

Specifically, suppose our category \(\cc\) has pullbacks and a terminal object \(T\). For any pair of objects \(A, B\) in \(\cc\), suppose we take the pull back on the morphisms \(t_A: A \to T\) and \(t_B: B \to T\). This then give rise to an object \(P\) equipped with two morphisms \(p_1: P \to A\) and \(p_2: P \to B\), universal in the sense demonstrated below.

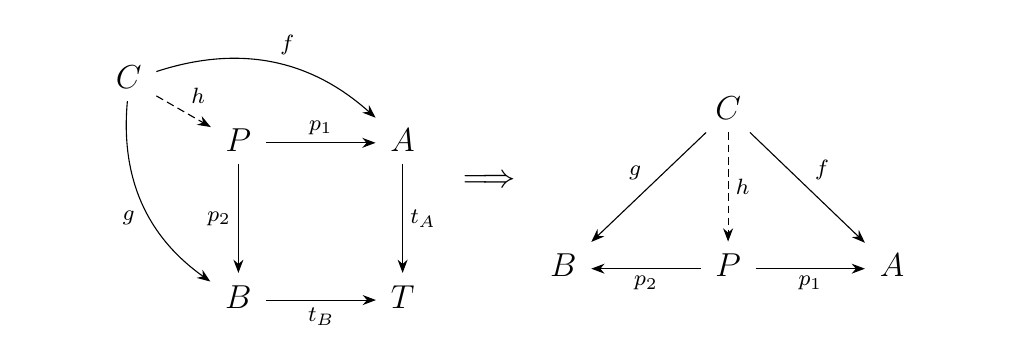Now on the top left we have our pull back. However, on the top right, we've unraveled the pullback and ignored the terminal object to observe that \(P\) has the universal property of what a product would demand. Hence we may denote \(P = A \times B\) as the product. Thus by Proposition \ref{prop_category_finite_products} \(\cc\) has all finite products. \textcolor{NavyBlue}{Note that we wouldn't have been able to construct this if we didn't have a terminal object; For example, if \(\cc\) was a discrete category, we wouldn't even have any morphisms to take a pullback on!}

Now to derive equalizers, consider a pair of parallel morphisms \(f, g: A \to B\). Then we may simply take their pullback to obtain the diagram below.

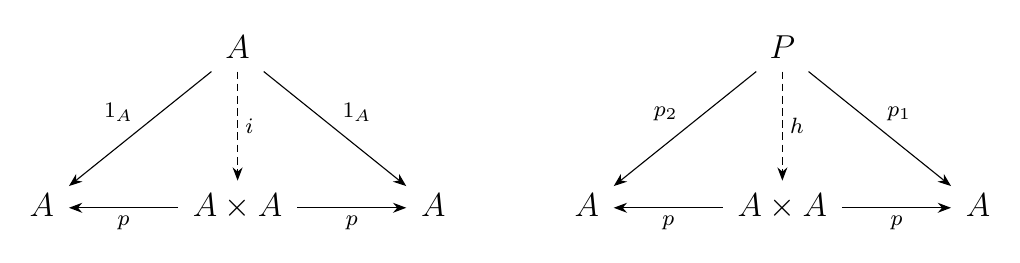
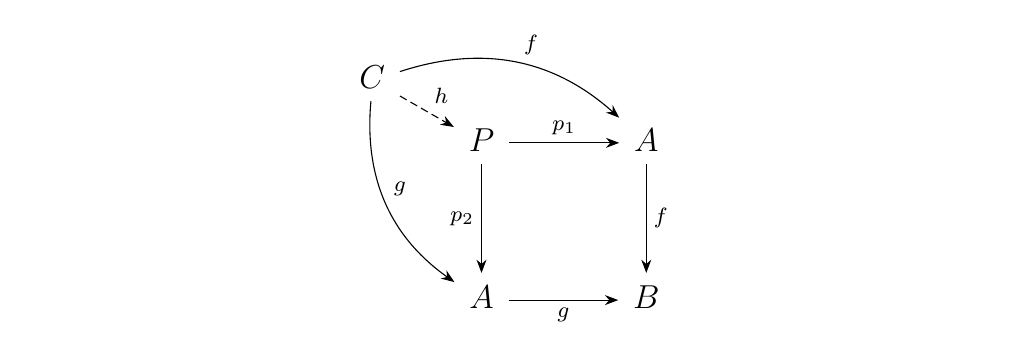If \(p: A \times A \to A\) is the natural projection map, then because we have a trivial mapping \(1_A: A \to A\), there exists a canonical canonical map \(i: A \to A \times A\) such that \(p \circ i = 1_A\). Similarly, because we have mappings \(p_1, p_2: P \to B\), we must have a mapping \(h: P \to A \times A\).

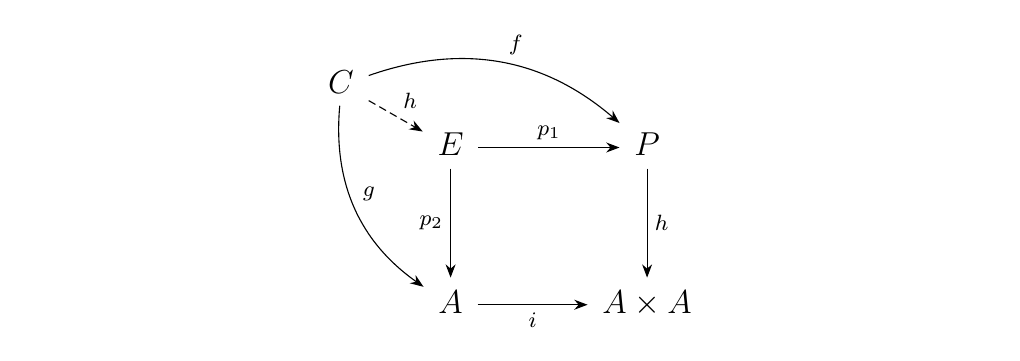
Now we can take the pullback on the morphism \(h: P \to A \times A\) and \(i: A \to A \times A\) to obtain the equalizer.

Hence we see that for finite limits, we can reduce our assumptions to pullbacks and a terminal object, giving rise to the final corollary.

If a category has pullbacks and a terminal object, then it has all finite limits.