2.7. Quotient Categories
The quotient category is a concept that generalizes the ideas of forming quotient groups, rings, modules, and even topological spaces. The core idea of obtaining a quotient "object" revolves around the concept of an equivalence class.
For example, in constructing the quotient group, one can go about constructing it in two different ways. One is easy, in which you simply form the concept of a coset, and then observe that nice things happen when you make cosets with normal subgroups. The hard way is to construct an equivalence relation, which gives rise to what we recognize as the concept of a coset, and then continuing further to create the quotient groups from normal subgroups. Both ways are equivalent, but one ignores the crucial and powerful idea of equivalence relations.
Let \(\cc\) be a locally small category. Suppose \(R\) is a function which, for every
pair of objects \(A, B\), assigns equivalence
relations \(\sim_{A, B}\) on the hom set \(\hom_{\cc}(A, B)\). Then we may define the
quotient category \(\cc/R\) where
- Objects. The same objects of \(\cc\).
- Morphisms. For any objects \(A,B\) of \(\cc\), we set \(\hom_{\cc/R}(A, B) = \hom_{\cc}(A, B)/\sim_{A, B}\).
Thus we see that morphisms between \(f: A \to B\) in \(\cc\) becomes equivalence classes
\([f]\) in \(\cc/R\).
With that said, we can naturally define a canonical functor \(Q: \cc \to \cc/R\) where \(Q\) acts identically on objects and where \(Q(f: A \to B) = [f] \in \hom_{\cc/R}(A,B)\). This in fact defines a functor if we observe that, for a pair of composable morphisms \(g, f\).
A nice property of this functor is the fact that if \(f \sim f'\), then \(Q(f) = Q(f')\). What is even nicer about this functor is that it has the following property.
Let \(\cc\) be a locally small category with an equivalence relation \(\sim_{A, B}\) on each set \(\hom_{\cc}(A, B)\). Then for any functor \(F: \cc \to \dd\) into some category \(\dd\) such that \(f \sim f'\), \(F(f) = F(f')\), there exists a unique functor \(H: \cc/R \to \dd\) such that \(H \circ Q = F\); or, diagrammatically, such that the following diagram commutes.
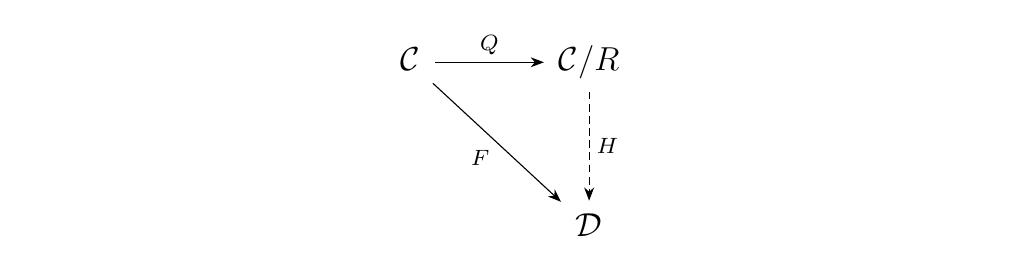
Observe that one functor \(H: \cc/R \to \dd\) that we can supply, which will have the above diagram commute, is one where \(H(C) = F(C)\) on objects and where for any \([f] \in \hom_{\cc/R}(A, B)\),
where \(f\) is an representative of the equivalence class \(f\). Note that this is well defined since \(F(f) = F(f')\) if \(f \sim_{A,B} f'\); hence this will appropriately send equivalent elements to the same morphism. It is not hard to show that it's unique; one can just suppose such an \(H\) exists and then demonstrate that it behaves like the functor we proposed initially.