1.5. Paths and Diagrams in Categories

In this section we give an overview of the concept of a path and of a diagram within a category, which are concepts that are exactly what they sound like. This is usually a discussion that is usually glossed over, which is a huge mistake since diagrams are used everywhere in mathematics. They'll appear in nearly every section from this point on, and any good book on category theory will have dozens of diagrams. In short, they are extremely indespensible.

So, we set off to do a justice to the important concepts of paths and diagrams. However, I've kept the pragmatic reader in mind and have avoided making this discussion abstract and irrelevant.

First, we form some intuition on what exactly a diagram is. Informally, a diagram in a category \(\cc\) consists of a finite sequence of arrows between objects. Below are some diagrams.

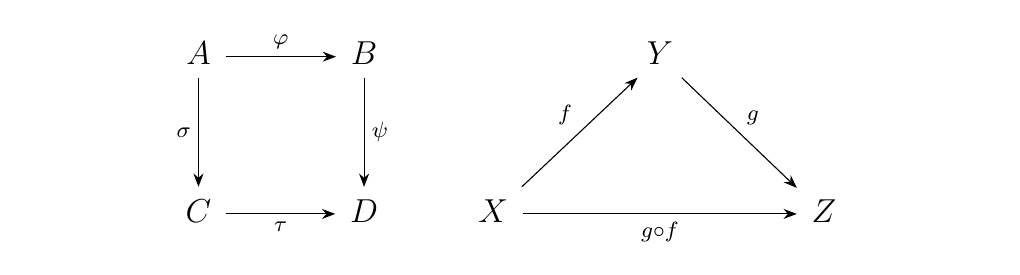We can also have more complicated diagrams such as the diagrams below.

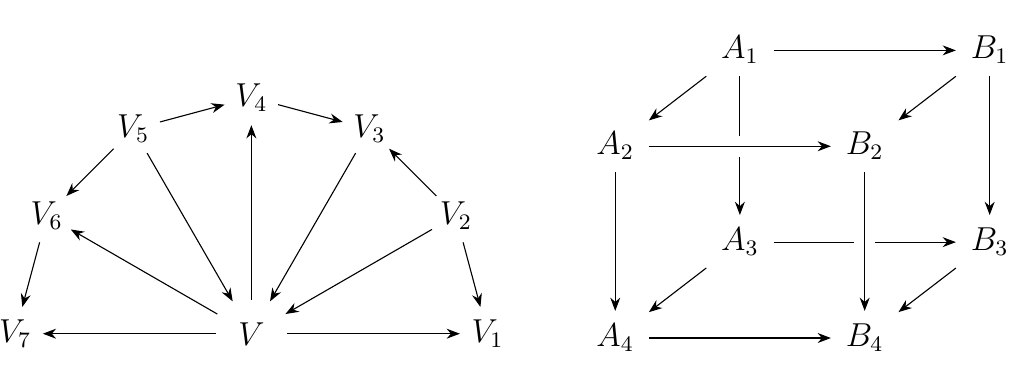Of course, a diagram does not really mean anything on its own; it is simply a graph\footnote{Technically, since a diagram can have multiple morphisms between two objects, every diagram is a "quiver." This is explored more in Chapter 2.}. A diagram requires the context of a category to have any meaning. Despite this, we can still abstract the core ingredients of what a diagram really is for a general category \(\cc\). To do so requires observing that in the diagrams above (which are the ones we care about), there are certain paths given by iterated composition. Thus we start at this concept and build upwards to define a diagram.

Let \(\cc\) be a category and consider two objects \(A\) and \(B\). A path \(p\) in \(\cc\) of length \(n\) from \(A\) to \(B\) consists of

• distinct objects \(A_1, A_2, \dots, A_{n+1}\) with \(A_1= A\) and \(A_{n+1} = B\)
• a chain of morphisms \(f_1: A_1 \to A_2, \dots, f_{n}: A_{n} \to A_{n+1}\)

and we say \(p = f_n \circ \cdots \circ f_1\). If two paths \(p = f_n \circ \cdots f_1\) and \(q = g_m \circ g_{m-1} \circ \cdots \circ g_1\) start and end at the same objects \(A\) and \(B\), we say \(p\) and \(q\) are parallel paths. For example, we have a path of length five from \(A_1\) to \(A_6\) in some category \(\cc\) displayed below in blue.

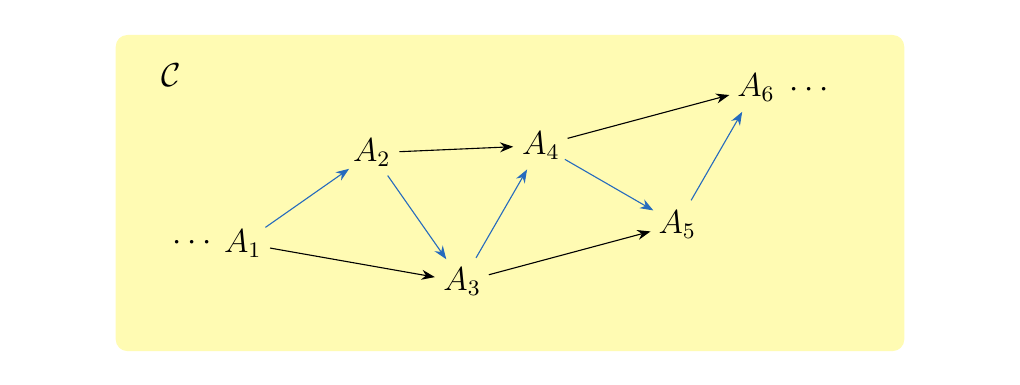
Note that in the above picture, we will in general have many possible paths between two different objects. We now face the question: is there a way to organize this data without getting too complicated?

To answer that question, we must work with a small category in order to avoid contradictions that arise due to size issues in set theory. With that said, we propose the following definition.

Let \(\cc\) be a small category. For any two objects \(A, B\), and for any positive integer \(n\), define the path set of order \(n\) from \(A\) to \(B\) as

\[ \path^n(A, B) = \{ \text{all paths } p: A \to B \text{ of length } n \}. \]

The above definition makes sense, but admittedly it is not illuminating. Is there another perspective we can make from this?

Yes! Because paths are made of components which are inherently ordered, one way to imagine a path is as a tuple \((f_1, \dots, f_n)\) of \(n\)-morphisms where the codomain of \(f_i\) is the domain of \(f_{i+1}\).
In other words, a path from \(A\) to \(B\) is an element of

\[ \hom(A, A_1)\times \hom(A_1, A_2)\times \cdots \times \hom(A_n, B). \]

for some objects \(A_1, \dots, A_n\) in \(\cc\). Therefore, we can say that

\[ \path^n(A,B) = \bigcup_{A_1, \dots A_n \in \text{Ob}(\cc)} \hom(A, A_1)\times \hom(A_1, A_2)\times \cdots \times \hom(A_n, B). \]

where in the above union we vary across all objects \(A_1, \dots, A_n \in \ob(\cc)\). Note that when \(n = 1\), we have that \(\path^n(A, B) = \hom(A, B)\). In this way, the path set can be thought of as a generalized hom-set.

A simple diagram \(J\) in a category \(\cc\) consists of two distinguished objects \(\textcolor{NavyBlue}{A}\) and \(\textcolor{Orange}{B}\), referred to as the source and target of \(J\), and any finite collection of parallel paths \(p_1: A \to B, p_2: A \to B, \dots, p_n: A \to B\) of any length.

Some simple diagrams are pictured below. In the first diagram, the source and targets are \(X\) and \(Z\); in the second, they are \(A\) and \(F\); in the third, they are \(V\) and \(V_7\).

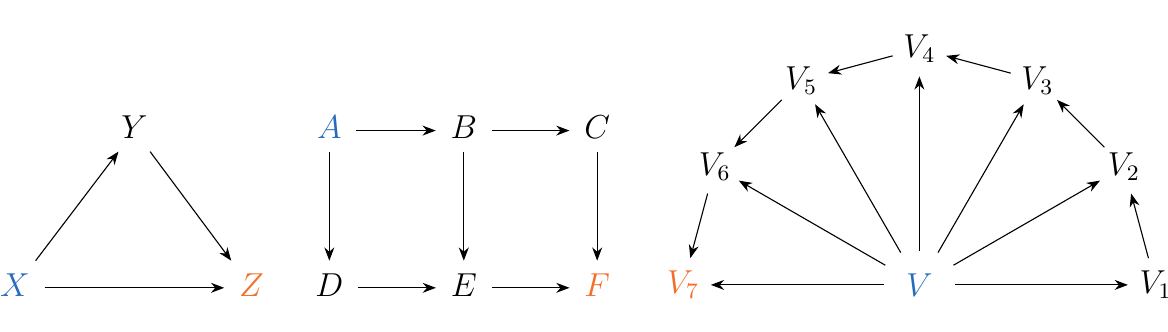In many situations, simple diagrams are what we really care about. This is because often times we have two objects of interests, and we consider many possible paths between them. And in those situations, we are generally asking: are all such paths equivalent?

This is something high schoolers ask themselves all the time, and a mistake they make all the time. Let \(n \ge 2\). Consider the functions

• \(e: \mathbb{N} \to \mathbb{N}\) where \(f(a) = a^n\) (\(e\) for exponent)
• \(p: \mathbb{N}\times \mathbb{N} \to \mathbb{N}\) where \(f(a,b) = a + b\) (\(p\) for plus)

Often times, they get confused and think that the paths of the diagram below are equivalent.

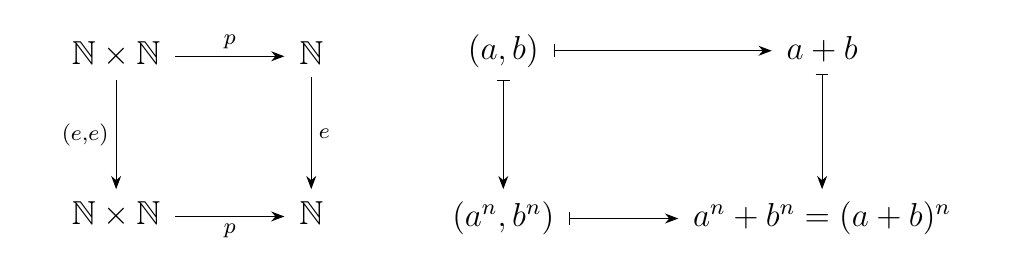Sadly, this equation does not hold generally, and the two paths of the diagram are not equivalent. Thus at this point we introduce terminology for discussing when paths are equivalent.

Let \(J\) be a simple diagram in \(\cc\). If every parallel path is equal, then we say \(J\) commutes and is a commutative diagram.

At this point, we should note that there is still some work to be done, since of course not all "diagrams" that we care about are simple. For example, an extremely important diagram that will eventually become engrained in your brain is pictured below on the left.\footnote{Understanding this diagram right now is not important; there is a lot more stuff one needs to learn before we get into what this means. Long story short, it is the universal property of a product.}

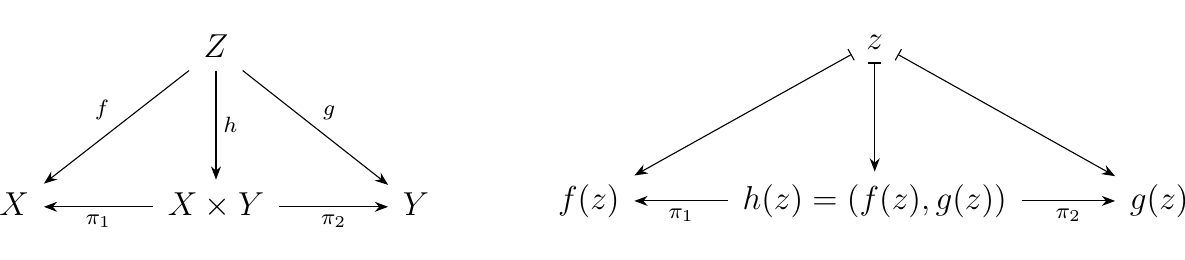Here, the objects are sets, and the morphisms are functions; the underlying function maps are pictured above on the right.

Clearly this diagram is not simple. However, note that it is built from simple diagrams; specifically, the left and right triangles are simple diagrams. At this point, it is clear that the task of rigorously defining the notion of
a diagram is reduced to defining what exactly we mean by "building" such diagrams.

{\large Exercises \vspace{0.2cm}}

• 1. Consider a category \(\cc\) with objects \(A, A_0, \dots, A_n, B, B_0, B_1, \dots, B_m\). Let \(A_0 = B_0 = A\) and \(A_n = B_m = B\), and suppose we have a family of
  isomorphisms \(f_i: A_{i-1} \isomarrow A_i\) and \(g_i: B_{i-1} \isomarrow B_i\) as below.

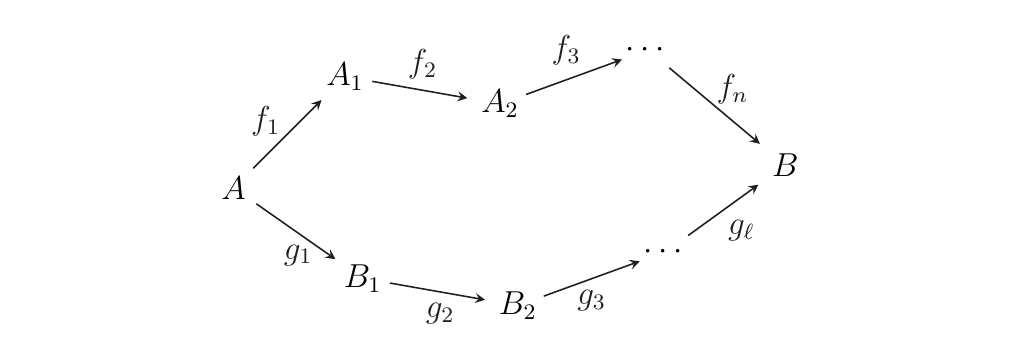Suppose we have another object \(C\) and isomorphisms \(\phi_i: A_i \isomarrow C\), \(\psi_i: B_i \isomarrow C\) with \(\psi_0 = \phi_0\) and \(\phi_n = \psi_m\). Prove that if \(\phi_{i} \circ f_i = \phi_{i+1}\) and \(\psi_{i} \circ g_i = \psi_{i+1}\), then the above diagram is commutative in \(\cc\).