6.1. Filtered Categories and Limits
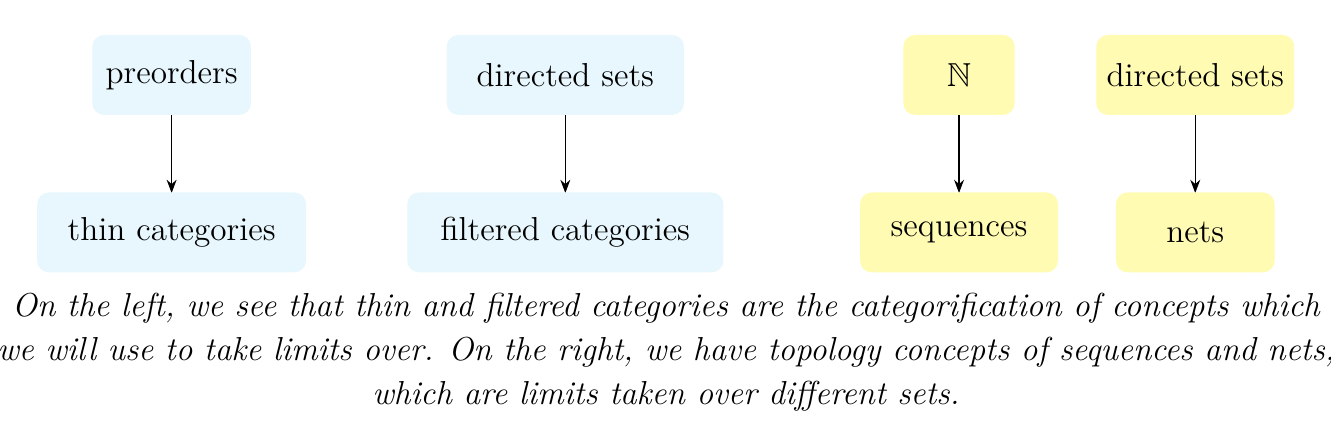
Outside of category theory, the most common types of limits that are taken in areas such as algebraic geometry and topology are inverse and directed limits. These are limits which are taken over thin categories (or preorders) which have at most one morphism between any two morphisms.
As we shall see, limits over thin categories do not possess the nice properties that limits taken over filtered categories have, which we will see is the categorification of the notion of a directed set. We will motivate our desire to work with filtered categories instead of just thin categories by observing an analogous motivation to work with directed sets instead of \(\mathbb{N}\) in sequences within topology. The picture in mind should be:
Let \(X\) be a topological space. Recall that a sequence \(\{a_n\}_{n=1}^{\infty}\) in \(X\) is a function \(a: \mathbb{N}\to X\) such that \(a(n) = a_n\). We say the sequence converges to a point \(x \in X\) if for every open set \(U\) of \(x\) there exists a \(N \in \mathbb{N}\) such that \(\{a_N, a_{N+1}, \dots, \} \subset U\).
Some of the first topological spaces that people worked with were metric spaces \((X, d)\), and the properties of these spaces were worked out over time. People eventually figured out that
- A subset \(F \subset X\) is closed if and only if \(F\) contains the limits of every sequence in \(F\).
- A subset \(U \subset X\) is open if and only if \(U\) contains does not contain the limit of any sequence in \(X - U\).
This is a wonderful result! However, it does not generalize to arbitrary topological spaces. There are weird counterexamples that we will not get into (cite An Introduction to Topology and Homotopy Theory by Sierdaski).
What this means is that sequences over a plain preorder (i.e., \(\mathbb{N}\)) are great, and they have nice properties, but they lack the ability to extend their nice properties to arbitrary topological spaces. We need more if we want it to work over arbitrary spaces.
This is where a directed set comes in.
A directed set \(D\) is a set equipped with a binary relation \(\le\) such that for all \(a, b, c \in D\),
- *1.* \(a \le a\) (Reflexive).
- *2.* if \(a \le b\) and \(b \le c\), then \(a \le c\) (Transitive)
- *3. For all \(a,b \in D\), there exists a \(c \in C\) such that \(a \le c\) and* \(b \le c\) (Directed).
The first two properties describe a preorder; only the last condition is new to us. To summarize, the "directed" axiom grants us an upper bounded in \(D\) for any finite set of elements of \(D\).
Let \(D\) be a directed set. Define a net, or Moore-Smtih Sequence, to be a function \(\lambda: D \to X\). We say a net \(\lambda\) converges to a point \(x \in X\) if for every open set \(U\) containing \(x\), there exists a \(d \in D\) such that \(\{\lambda(c) \mid c \ge d\} \subset U\).
Directed sets are then enough to give us the following theorem:
Let \(X\) be a topological space.
- A subset \(F \subset X\) is closed if and only if every convergent net \(\lambda: D \to X\) has a limit in \(F\)
- A subset \(U \subset X\) is open if and only if every convergent net \(\lambda: D \to X - U\) does not have a limit in \(U\).
Hence we see that limits taken over preorders have substantial benefits than when they are simply taken over \(\mathbb{N}\). Similarly, what we will see is that limits taken over filtered categories enjoy much better properties than limits simply taken over preorders. First, we introduce filtered categories.
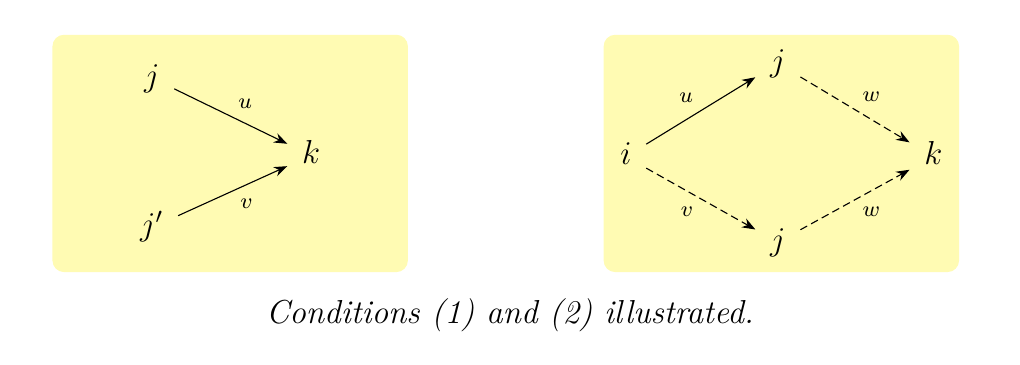
We say that a category \(J\) is filtered if
- *1.* For any pair of objects \(j, j'\), there exists an object \(k\) and morphism \(u:j \to k\) and \(v: j' \to k\).
- *2.* For any pair of parallel morphism \(u, v: i \to j\), there exists an object \(k\) and a morphism \(w: j \to k\) such that the diagram below commutes.
We do not say the empty category is filtered; this should be obvious, but it also needs to be said.
Let \(J\) be a thin category. What does it take for \(J\) to be filtered? Well, in a thin category, there is never any pair of distinct morphisms. Hence condition (2) is trivial. Therefore, for \(J\) to be filtered, we simply need to satisfy (1). But in the language of thin categories, condition (1) can be read as "for any \(j, j \in J\), there exists a \(k\) such that \(j, j' \le k\)". Such a condition holds if and only if \begin{center} every finite subset \(S \subset J\) has an upper bound in \(J\). \end{center}Thus, a thin category \(J\) needs to have the above property in order to be a filtered category.
An example of this concerns the category \(**Open**(X)\), where \(X\) is a topological space. The objects are open sets, while morphisms are inclusions. The maximal element \(X \in **Open**(X)\) always exists, and hence makes this thin category filtered.
\chapterimage{chapter7_pic/chapt7head.pdf}