2.4. Vertical, Horizontal Composition; Interchange Laws

In the previous section, we considered the idea of forming a composition of natural transformations, and we verified that this formed a valid natural transformation. That is, if we have three functors $F, G, H : \cc \to \dd$ between two categories $\cc$ and $\dd$, and if $\sigma: F \to G$ and $\tau:G \to H$ are natural transformations, then we can form the natural transformation

\[ (\tau \circ \sigma) : F \to H. \]

We call such a type of composition as vertical compositions of natural transformations, since the idea can be captured in the following diagram.

\begin{minipage}{0.8\textwidth} \vspace{0.5cm}

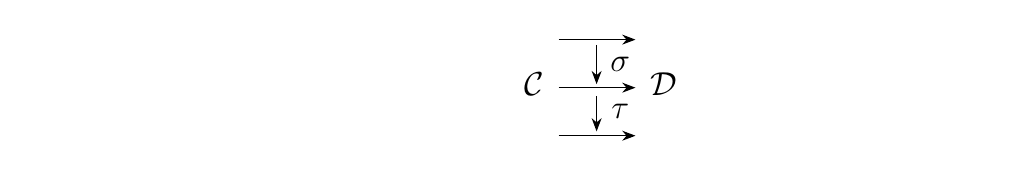\end{minipage} \vspace{0.3cm}

We can also perform a different, but similar type of composition between natural transformations. Suppose $F, G: \bb \to \cc$ and $F', G': \cc \to \dd$ are functors between categories $\bb, \cc$, and $\dd$. Furthermore, suppose we have natural transformations $\eta: F \to G$ and $\eta': F' \to G'$. Then we have diagram such as the following.

\begin{minipage}{0.7\textwidth} \vspace{0.5cm}

\hspace{5cm}
\end{minipage} \vspace{-0.5cm}

Now let $B$ be an object of $\bb$. There are two ways we can transfer this object to an object of $\cc$; namely, via mappings of $F$ and $G$. Thus $F(B)$ and $G(B)$ are two objects of $\cc$. Since $\eta: F \to G$ is a natural transformation between these objects, we see that there's a way of mapping between these two elements in $\cc$:

\[ \eta(B): F(B) \to G(B). \]

Hence, we have two objects in $\cc$ and a morphism in between them. Hence, we know that the natural transformation $\eta': F' \to G'$ implies the following diagram commutes.

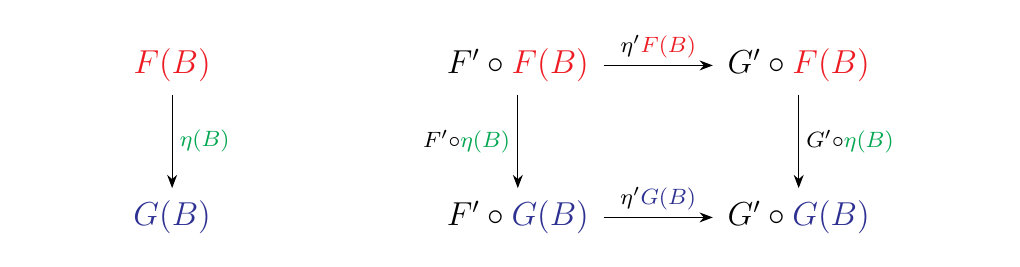Note that in the last diagram, all of the objects and morphisms between them exist in $\dd$. The easiest way to see why this diagram commutes is to go back directly to the definition of a natural transformation; namely, the pair of objects along with their morphism on the left imply the commutativity of the diagram on the right.

This can be done in general for categories $\bb, \cc$, and $\dd$ which have functors $F, G:\bb \to \cc$ and $F', G': \cc \to \dd$ associated with natural transformations $\eta: F \to G$ and $\eta': F' \to G'$. Furthermore, it holds for all $B \in \bb$.

Note further that this diagram is similar to a diagram which represents a natural transformation; but between which functors? If we look closely, we see that it is between $F\circ F'$ and $G \circ G'$.

This leads us to make the following formulaic definition: For natural transformations $\eta: F \to G$ and $\eta': F' \to G'$ such that $F, G: \bb \to \cc$ and $F',G' : \cc \to \dd$, then for $B \in \bb$ we define their "horizontal" composition as the diagonal of the above diagram; that is,

\[ (\eta \circ \eta')B = G'(\eta(B)) \circ \eta' F(B) = \eta'(G(B))\circ F'(\eta(B)). \]

The above diagram doesn't quite show that $\eta \circ \eta': F' \circ F \to G \circ G' $ is a natural transformation. In order to do this, we need to start from two objects in $\bb$ and consider a morphism between them.

The function $\eta \circ \eta':F\circ F' \to G \circ G'$ is a natural transformation between the functors $F'\circ F, G' \circ G: \bb \to \dd$.

To show this, we consider a morphism $f: B \to B'$ between two objects $B$ and $B'$ in $\bb$. We then claim that the following diagram is commutative:

First, observe that the left square is commutative due to the fact that $\eta$ is a natural transformation from $F$ to $G$. Therefore, it produces a commutative square diagram, and we obtain the above left square diagram by applying $F'$ to the commutative diagram produced by $\eta: F \to G$.

The right square in the diagram is obtained by the fact that $\eta'$ is a natural transformation between functors $F'$ and $G'$. Hence the diagram is commutative, and it acts on the objects $G(B)$ and in $\cc$. Therefore, we see that $\eta \circ \eta'$ is a natural transformation.

\textcolor{NavyBlue}{Thus we see that we have "horizontal" and "vertical" notions of composing natural transformations. Let us denote "horizontal" transformations as $\circ$ and "vertical" transformations as $\cdot$ between natural transformations.}

It is also notationally convenient to denote functor and natural transformation compositions as

\[ F' \circ \tau : F' \circ F \to F' \circ T \quad \eta' \circ G: F' \circ G \to G' \circ G \]

which are two additional natural transformations. \textcolor{purple}{(Remember we showed that the left square in the commutative diagram of the previous proof commuted by observing that it was obtained by the commutative diagram produced by the natural transformation $\eta$ and composing it with $F'$? What we really showed is that $F' \circ \eta$ is a natural transformation, since this natural transformation described that square. Similarly, $\eta' \circ G$ is the natural transformation which represents the right square of the commutative diagram in the previous proof.)}

With the above notation, we can then write that

\[ \eta' \circ \eta = (G' \circ \eta) \cdot (\eta' \circ F) = (\eta' \circ G) \cdot (F' \circ \eta). \]

This idea of ours can be extended to a more general situation. Suppose we have instead three categories $\bb, \cc$, and $\dd$ and where $F, G, H: \bb \to \cc$ and $F, G, H: \cc \to \dd$ are functors associated with natural transformations $\eta: F \to G, \sigma : G \to H$, and $\eta': F' \to G', \sigma': G' \to H'$. The following diagram may be more helpful than words: \

\begin{minipage}{0.65\textwidth}

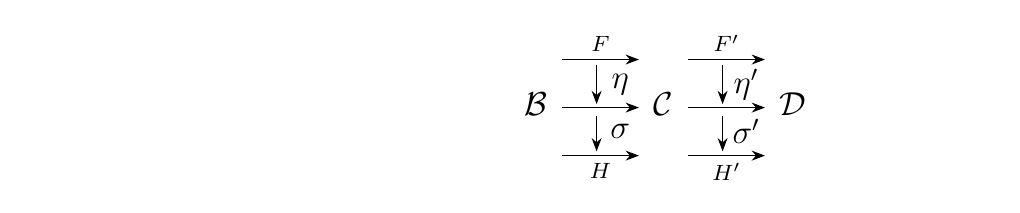\hspace{7cm}
\end{minipage} \vspace{-0.5cm}

Note we've omitted the label of $G$ and $G'$ on the middle horizontal arrows since they don't exactly fit in there when we include the labels for the natural transformations.

Now suppose we have an object $B$ in $\bb$. Then we can create three objects $F(B), G(B)$ and $H(B)$ in $\cc$, and we may interchange between these objects via the given natural transformations. Specifically, $\eta(B) : F(B) \to G(B)$ and $\sigma(B): G(B) \to H(B)$. However, we also know that $\eta', \sigma'$ are natural transformations between $\cc$ and $\dd$, and hence imply the following commutative diagram.

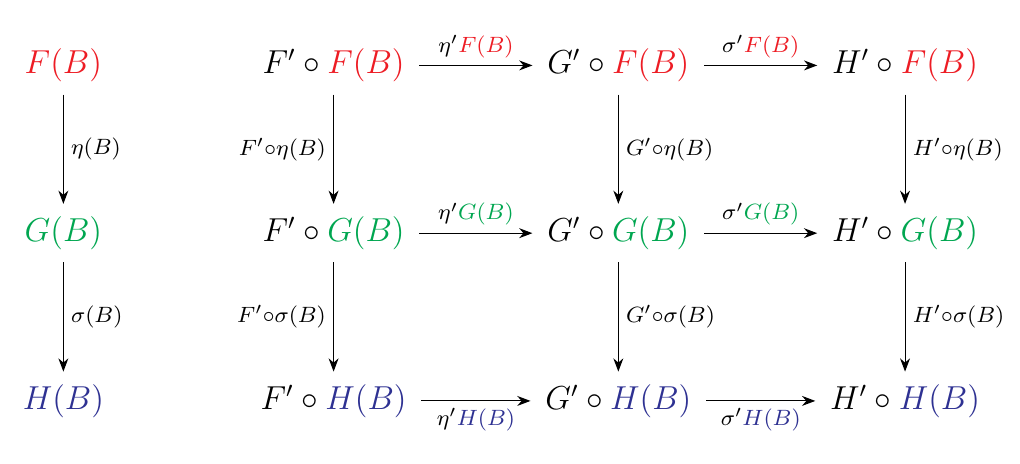Suppose we start at the upper left corner and want to achieve the value at the bottom right. There are two ways we can do this: We can travel within the interior of the diagram, or we can travel on the outside of the diagram.

In traveling on the interior of the diagram, note that the composition of the arrows of the upper left square is $\eta' \circ \eta$. In addition, composition of the arrows of the bottom right square is $\sigma' \circ \sigma$.

In traveling on the exterior of the diagram note that the composition of the top row is $\eta' \cdot \sigma'$ and composition of the right most vertical arrows is $\eta \cdot \sigma$. Since both paths achieve the same value, we see that

\[ (\eta' \cdot \sigma') \circ (\eta \cdot \sigma) = (\eta' \circ \eta) \cdot (\sigma' \circ \sigma) \]

which is known as the Interchange Law.

This leads us to make the following definition.

We define a double category to be a set of arrows which obey two different forms of composition, generally denoted as $\circ$ and $\cdot$, which together satisfy the interchange law.

Furthermore, a 2-category is a double category in which $\cdot$ and $\circ$ have the same exact identity arrows.