1.11. Initial, Terminal, and Zero Objects
We can also be more specific in discussing the nature of the objects of a given category \(\cc\).
Let the following objects exist in some category \(\cc\).
- Let \(T\) be an object. Then \(T\) is terminal if for each object \(A\), there exists exactly one morphism \(f_A\) such that \(f_A: A \to T\).
- Let \(I\) be an object. Then \(I\) is said to be initial if for each object \(A\) there exists exactly one morphism \(f_A : I \to A\).
- An object \(Z\) is said to be a zero object if it is both terminal and initial. Since terminal and initial objects are unique, so is a zero object.
Equivalently, it is zero if for any objects \(A, B\), there exists exactly one morphism \(f: A \to Z\) and exactly one morphism \(g: Z \to B\). Hence, for any two objects there exists a morphism between them, namely given by by \(g \circ f\), called the zero morphism from \(A\) to \(B\).
If an object \(T\) is terminal, then there is one and only morphism to itself (namely, its identity). Therefore, for any two terminal objects \(T\) and \(T'\), they are isomorphic, since by assumption there exists unique morphisms \(f: T \to T'\) and \(g: T' \to T\) and we have no choice but to say
Recall that in the category \(\grp\), there exists a trivial group \(\{e\}\). Moreover, for each group \(G\), there exist unique group homomorphisms
and
Note that both are group homomorphisms since they both behave on identity elements and are trivially distributive across group operations. This then shows that \(\grp\), the trivial group is initial and terminal and hence a zero object.
This makes sense since for any two groups \(G, H\), there exists a unique map
which could be factorized as
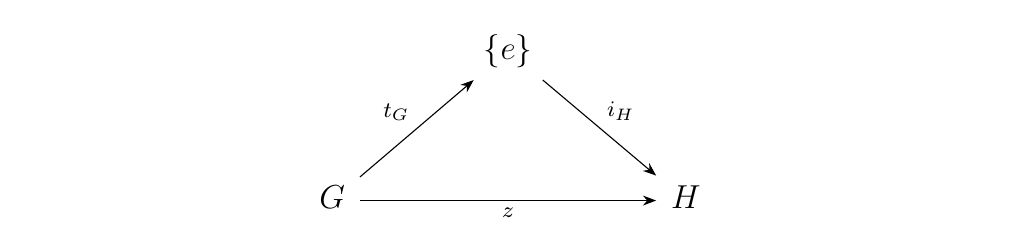 which demonstrates the existence of a zero object (the name "zero" makes sense now, right?),
which we already know is \(\{e\}\).
Note in this example, we did not actually use much group theory. In fact, this could be repeated
for the categories \(R\rmod\), \(\ab\), and other similar categories.
which demonstrates the existence of a zero object (the name "zero" makes sense now, right?),
which we already know is \(\{e\}\).
Note in this example, we did not actually use much group theory. In fact, this could be repeated
for the categories \(R\rmod\), \(\ab\), and other similar categories.
The next two examples demonstrate that terminal and initial objects of course don't always have to coincide like they did in the previous example.
Let \(n\) be a positive integer. Recall that we can create a category, specifically a preorder, by taking our objects to be positive integers less than \(n\), and allowing one morphism \(f: k \to m\) whenever \(k \le m\).
 Then 1 is an initial object while \(n\) is a terminal object. This
is because for any number \(1 \le m \le n\), there exists a unique morphism
from \(1\) to \(m\), and a unique morphism \(m\) to \(n\), both which may
be obtained by repeated composition.
Then 1 is an initial object while \(n\) is a terminal object. This
is because for any number \(1 \le m \le n\), there exists a unique morphism
from \(1\) to \(m\), and a unique morphism \(m\) to \(n\), both which may
be obtained by repeated composition.
Consider the category \(\Set\). Let \(X\) be a given set in this category. Then there are two unique functions which we may construct. First, there is the function
where everything in \(X\) is mapped to the one element \(\bullet\) of the one point set. Secondly, we may construct a function whose domain is the empty set, and whose codomain is \(X\), as below.
Thus we have that, in \(\Set\), the one point set is a terminal object \(\{\bullet\}\) while the empty set \(\varnothing\) is an initial object.
One may wonder at this point: How exactly is \(i_X\) a true, set theoretic function? And why can't we also obtain a unique morphism \(i'_X: X \to \varnothing\), so that \(\varnothing\) is a terminal object as well?
The second question is easy to answer; if \(\varnothing\) was also terminal, then we'd have that \(\{\bullet\} \cong \varnothing\) which is not true. Since this is a bit of a boring answer, we'll explain in detail.
Recall that a function in \(f: A \to X\) between two sets \(A\) and \(X\) is a relation \(R \subset A \times X\) which satisfies two properties.
- 1. (Existence.) For each \(a \in A\), there exists a \(x \in X\) such that \((a, x) \in R\)
- 2. (Uniqueness. Or, if you'd like, the vertical line test.) If \((a, x) \in R\) and \((a, x') \in R\) then \(x = x'\).
Now observe that if \(A = \varnothing\), then \(R \subset \varnothing \times X = \varnothing\). Hence (1) and (2) are satisfied because each is trivially true. However, we don't get a function \(f: X \to \varnothing\), since in this case (1) fails. Specifically, (1) demands the existence of elements in our codomain, a demand we cannot meet if it is empty.
Thus we see that \(\varnothing\) is initial, but not terminal as our intuition may suggest, and that \(\{\bullet\}\) is terminal.
Consider the category of fields \(\fld\). Suppose we ask if this has an initial or terminal object.
We might guess that the smallest field
which has characteristic 2 is an initial object. However, this fails to be initial. Observe that the only homomorphism between \(\mathbb{F}_2\) and \(\mathbb{F}_3\) is the zero homomorphism, which is not in our category. (Recall that \(\fld\) is a full subcategory of \(\ring\), a category whose morphisms we require to be unit preserving.)
The reason why it must be the zero homomorphisms is because \(\mathbb{F}_3\) has characteristic three, and in general, two fields will only share a (nonzero) field homomorphisms if they have the same characteristic.
By a similar argument, we can state that terminal objects also do no exist. Overall, these objects fail to exist in \(\fld\) because fields have a large set of restictions imposed by their numerous axioms. Hence, this category lacks initial and terminal objects.
{\large Exercises \vspace{0.5cm}}
-
*1.*
- (i.) Let \(\cc\) be a category with initial object \(I\). For any two objects \(A, B \in \cc\), define for each \(f \in \hom_{\cc}(A, B)\) the functor
\[ P_f: **2** \to \cc \]such that \(P(\textcolor{NavyBlue}{\bullet}) = A\), \(P(\textcolor{Orange}{\bullet}) = B\), and \(P_f(\textcolor{NavyBlue}{\bullet} \to \textcolor{Orange}{\bullet}) = f: A \to B\). Show that for each \(f: A \to B\) in \(\cc\), we have a natural transformation
\[ \eta: P_{1_I} \to P_f. \]Note that \(1_I: I \to I\) is the identity on the initial object. * (ii.) Suppose we don't know if \(\cc\) has an initial object, but we have a distinguished object \(I'\) with the property that for each \(f \in \hom_{\cc}(A,B)\) there is a natural transformation
\[ \eta: P_{1_{I'}} \to P_f. \]Is \(I'\) an inital object? * (iii.) Dualize your work for terminal objects.\ (Hint: We now want a natural transformation \(\eta': P_f \to P_{1_I})\).
\chapterimage{chapter2_pic/chapt2head.pdf}