1.8. Isomorphism Theorems

With our knowledge of homomorphisms, normality and quotient groups, we are now able to develop four important theorems, known as the isomorphism theorems, which are indispensible tools in group theory. The isomorphism theorems give isomorphic relations which we can use to our advntage to understand groups and aid our proofs.

The isomorphism theorems are very deep theorems in abstract algeba. While one may go deeper into algebra, they will come across isomorphism theorems analagous to the ones below again and again.

[ (First Isomorphism Theorem)] Let $\phi: G \to G'$ be a homomorphism. Then

\[ G/\mbox{ker}(\phi) \cong \mbox{im}(\phi). \]

\vspace{-5mm} This is one of the more useful isomorphism theorems, and says something that matches out intuition. That is, if we quotient out the $\mbox{ker}(\phi)$, i.e., the set of all elements which get mapped to 0, then we should obtain something isomorphic to $\mbox{im}(\phi)$.

\textcolor{Plum}{We'll prove this directly. That is, we'll create a homomorphism between $G/\ker(\phi)$ and $\im(\phi)$, and then show that this homomorphism is one-to-one and onto, and therefore bijective. Thus the groups will be isomorphic.}

Let $\phi: G' \to G$ be a homorphism. Write $K = \ker(\phi)$. Define $\psi: G/K \to \im(\phi)$ as

\[ \psi(gK) = \phi(g) \]

where $gK \in G/K$ and $g \in G$.

(\textcolor{red}{We'll use left cosets ($gK$) to talk about elements in $G/K$ to remind the reader that left cosets can be used to characterize a quotient group just as as right cosets can.})

\textcolor{NavyBlue}{We want this to be a homomorphism. But we pulled this function out of nowhere, so let's check if this is well-defined.}

Well-Defined. Suppose $g' \in gK$. Then $gK = g'K$, and our goal will be to show that $\psi(gK) = \psi(g'K)$. Since $g' \in gK$, there exists a $k \in K$ such that $gk = g'$. Then

\[ \psi(g'K) = \psi((gk)K) = \psi(gK) = \phi(g) \]

while

\[ \psi(gK) = \phi(g). \]

Therefore $\psi(g'K) = \psi(gK)$, so the representative $g$ or $g'$ does not matter.

\textcolor{NavyBlue}{Now that we know this function is not nonsense, we move on to showing it is a homomorphism.}

It's a Homomorphism. Let's justify that this is a homorphism. For $gK, g'K \in G/K$,

\[\begin{align*} \psi(gK \cdot g'K) = \psi((gg')K) = \phi(gg')\\ = \phi(g)\phi(g') = \psi(gK)\psi(g'K) \end{align*}\]

where in the second step we used the fact that $\phi$ itself is a homomorphism. Thus we have that $\psi$ is a homomorphism.

\textcolor{NavyBlue}{We'll now show this is a bijective homomorphism, thereby proving the desired isomorphism.}

One-to-One. To show this is one-to-one, we can use Theorem 1.\ref{theorem_isomorph}. Thus our goal will be to show that $\ker(\psi) = \{e_G\}$, the identity element of $G$.

Suppose

$$ \psi(gK) = e $$ which is the identity in $\im(\phi)$ (technically, the identity in $G'$). Then by construction $\phi(g) = e.$ However, this holds for all $g \in K$ (as this is the kernal of $\phi$). Therefore $\ker(\psi) = \{gK \mid g \in K\} = \{K\}$. But $K$ is the identity in $G/K$. Thus by Theorem 1.\ref{theorem_isomorph}, we have that $\psi$ is one-to-one. * Onto. To show this is onto, we'll simply show that for any $h \in \im(\phi)$, there exists a $gK \in G/K$ such that $\psi(gK) = h$.

So consider any $h \in \im(\phi)$. By definition, $h = \phi(g)$ for some $g \in G$. Now observe that for the element $gK \in G/K$,

\[ \psi(gK) = \phi(g) = h. \]

Thus $\psi$ is onto.

\textcolor{Plum}{In total, we have showed the following: there exists a bijective homomorphism (i.e., an isomorphism) between $G/K = G/\ker(\phi)$ and $\im(\phi)$. Therefore $G/\ker(\phi) \cong \im(\phi)$ as desired.} The second isomorphism theorem summarizes a great deal of useful information concerning groups.

[ (Second Isomorphism Theorem)] Let $G$ be a group, $H$ a subgroup of $G$ and $N$ a normal subgroup of $G$. Then

1. $NH$ is a subgroup of $G$ ($HN$ is also a subgroup)
2. $N \normal NH$ (and $N \normal HN$)
3. $H \cap N \normal H$
4. $H/(H \cap N) \cong NH/N$ (and $H/(H \cap N) \cong HN/N$).

We put parenthesis in some of the statements because while they are true, most people state the second isomorphism theorem by either removing the text in parenthesis or only keeping the text in parenthesis. However, we don't want the reader to get the impression that, for example, $NH \le G$ but $HN \not\le G$. We think it is fair to be thorough and precise. \begin{minipage}{0.25 \textwidth} \begin{figure}[H]

\end{figure} \end{minipage} \hfill \begin{minipage}{0.7\textwidth} The diagram to the left demonstrates why the Second Isomorphism Theorem is also known as the diamond isomorphism theorem since a relationship between the four main objects in play can be created. \ The lemma below will clean up the proof of this theorem. \end{minipage}
\ \

\noindentLemma 1.7.1 Let $G$ be a group. Suppose $N \normal G$. Then for any $n \in N$, $h \in G$, there exists $n' \in N$ such that $hn = n'h$ and $nh = hn'$.

Proof: Since $N$ is normal, we know that for any $n \in N$, $hnh^{-1} \in N$ for any $h \in G$. In particular, this means that $hnh^{-1} = n'$ for some $n' \in N$. This implies that $hn = n'h$, which is what we set out to show. \

Now we prove the theorem itself. We'll only include proofs for the statments not in paranthesis, because the proofs of the statements in paranthesis are basically identical to the ones we'll offer for those not in paranthesis (e.g., for the proof that $NH \le G$, only small tweaks are needed to show that $HN \le G$).

We'll prove one statement at a time.

1. \textcolor{NavyBlue}{Consider $NH = \{nh \mid n \in N, h \in N\}$. This is clearly nonempty ($N, H$ are both nonempty), so we can use the Theorem 1.\ref{subgroup_test}, the subgroup test, to prove this.}

Let $n_1h_1, n_2h_2 \in NH$. Our goal is to show that $n_1h_1(n_2h_2)^{-1} \in NH$. Thus observe that

\[ n_1h_1(n_2h_2)^{-1} = n_1h_1h_2^{-1}n_2^{-1} = n_1hn_2^{-1} \]

where in the last step we know that $h_1h_2^{-1} = h$ for some $h \in H$. Since $N$ is normal, we have by Lemma 1.7.1 that there an $n^* \in N$ such that $hn_2^{-1} = n^*h$. Therefore,

\[ n_1(hn_2^{-1}) = n_1(n^*h) = (n_1n^*)h \in NH \]

Therefore we have that $n_1h_1(n_2h_2)^{-1} \in NH$, proving that $NH \le G$. * 2. \textcolor{NavyBlue}{We can prove this directly.} Let $nh \in NH$. By Lemma 1.7.1, we know that $nh = hn'$ for some $n' \in N$. Therefore

\[\begin{align*} (nh)N(n^{-1}h^{-1}) = (hn')N(n^{-1}h^{-1}) = h(n'Nn^{-1})h^{-1}\\ = hNh^{-1} = N \end{align*}\]

where in the last step we used the fact that $N$ is normal and invoked Theorem 1.10.2. By the same theorem, we can then conclude that $N \normal NH$. * 3. \textcolor{NavyBlue}{To prove this, first recall that $H \cap N$ is a a subgroup of $G$ since $H$ and $N$ are both subgroups.} Now let $a \in H \cap N$ and $h \in H$.

We can prove normality by Theorem 1.10.3, speficially, that $hah^{-1} \in H$ for all $a \in H \cap N$ and $h \in H$. But since $a \in H$, we already know that $hah^{-1} \in H$. So By Theorem 1.10.3, we thus have that $N \cap H \normal H$. * 4. \textcolor{NavyBlue}{To prove this last statement, we first construct a homomorphism $\phi: H \to NH/N$ by defining $\phi(nh) = Nh$.} This is a homomorphism since for $h, h' \in H$,

\[ \phi(nhnh') = Nhnh' = (Nh)(Nnh') = (Nh)(Nh') = \phi(h)\phi(h') \]

where in the second step we used the fact that (1) $N \normal NH$ and (2) $(Nh)(Nh') = N(hh')$ by Theorem 1.10.4.

\textcolor{Plum}{Note that $\phi$ is onto.} For any $Nh \in NH/N$, we note that any $nh \in NH$ maps to this element via $\phi$ for any $n$. Since this is onto, $\im(\phi) = NH/N$.

\textcolor{Plum}{Also, observe that $\ker(\phi) = H \cap N$}, since for any $h \in (H \cap N)$ we have that $\phi(h) = Nh = N$, which the identity in $NH/N$.

Now by the First Isomorphism Theorem, we have that

\[ H/\ker(\phi) \cong \im(\phi) \implies H/(H \cap N) \cong NH/N \]

as desired.

We now move onto the third isomorphism theorem, which matches our intution for when we form a quotient of quotient groups.

[ (Third Isomorphism Theorem)] Let $K, N$ be normal subgroups of $G$, with $N \le K$. Then $K/N \normal G/N$ and

\[ (G/N)/(K/N) \cong G/K. \]

\vspace{-0.5cm}

\textcolor{NavyBlue}{First we'll show that $K/N \normal G/N$. Consider any $Nk \in K/N$, where $k \in K$, and any $Ng \in G/N$, where $g \in G$. Our goal will be to show that $(Ng)(Nk)(Ng)^{-1} \in K/N$.}

\phantom{1} \hspace{0.5cm} Observe that

\[ (Ng)(Nk)(Ng)^{-1} = (Ng)(Nk)(Ng^{-1}) = N(gkg^{-1}) \]

where we used the fact that $N \normal G$.
Since $K \normal G$, we know that $gkg^{-1} \in K$. That is, $gkg^{-1} = k'$ for some $k' \in G$. Therefore, $N(gkg^{-1}) \in K/N$ so that $(Ng)(Nk)(Ng^{-1}) \in K/N$. Since $g, k$ were arbitrary, we have by Theorem 1.10.3 that $K/N \normal G/N$ as desired.

\textcolor{NavyBlue}{Next, we'll show that $(G/N)/(K/N) \cong G/K$. We'll do his by constructing an isomorphism between the two groups.}

\phantom{1} \hspace{0.5cm} Construct a homomorphism $\phi: G/N \to G/K$ defined as $\phi(Ng) = Kg$ where $Ng \in G/N$. First, we'll show this is a homomorphism. For any $Ng, Ng' \in G/N$, we have that

\[\begin{align*} \phi\big((Ng)(Ng')\big) = \phi(N(gg')) = Kgg' \\ = (Kg)(Kg') = \phi(Ng)\phi(Ng') \end{align*}\]

where in the third step we used the fact that $K \normal G$. Therefore, this is a homomorphism.

Next, observe that this is onto, since for any $Kg \in G/K$, we know that the element $Ng \in G/N$ maps to $Kg$ via $\phi$. Therefore $\im(\phi) = G/K.$

We'll now show that $\ker(\phi) = K/N$. Observe that

\[ \ker(\phi) = \{Ng: \phi(Ng) = K\} = \{Ng: Kg = K\} = \{Ng: g \in K\} = K/N. \]

Therefore, $\ker(\phi) = K/N$.

Finally, we can use the First Isomorphism Theorem to conclude that

\[ (G/N)/\ker(\phi) \cong \im(\phi) \implies (G/N)/(K/N) \cong G/K \]

as desired.

We now move onto the Fourth Isomorphism Theorem, which is one of the more powerful isomorphism theorems along with the First Isormorphism Theorem.

[ (Fourth Isormorphism Theorem)] Let $N \normal G.$ Then every subgroup of $G/N$ is of the form $H/N$ where $N \le H \le G$. Moreover, if $H, K$ are subgroups of $G$ and they contain $N$, then

1. $H \le K$ if and only if $H/N \le K/N$
2. $H \normal G$ if and only if $H/N \normal G/N$
3. if $H \le K$ then $[K:H] = [K/N:H/N]$
4. $(H \cap K)/N \cong (H/N) \cap (K/N)$.

\begin{minipage}{0.4\textwidth}

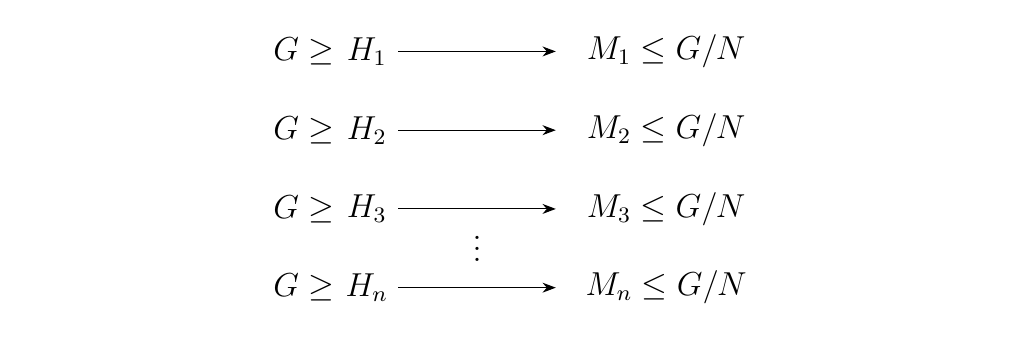
\end{minipage}\hfill \begin{minipage}{0.55\textwidth} The Fourth Isomorphism Theorem is also commonly known as the correspondence theorem, since what it effectively states is that there is a one-to-one correspondence between subgroups $H$ of $G$ which contain $N$ and the subgroups of $G/N$.

Thus, if $G$ has $n$ subgroups $H_i$ which contain $N$, then $G/N$ has $n$ subgroups. \end{minipage}

We first prove the first statement.

\textcolor{NavyBlue}{Our goal here will be to show that $M \le G/N \implies M = H/N$ where $M$ is some subgroup of $G/N$ and $N \le H \le G$.}

\phantom{1} \hspace{0.5cm} Consider a subgroup $M$ of $G/N$. Let $H$ be the set of all $h \in G$ such that $Nh \in M$. Then observe that $N \subset H$, since the smallest subgroup of $G/N$ is the trivial group, namely $\{N\}$. Therefore $N \subset H \subset G$.

\textcolor{NavyBlue}{Now we show that $N \le H \le G$. To do this, we just need to show that $H \le G$, which we will do by the subgroup test.}

Let $h, h' \in H$. Since $M \le G/N$, we know that for any $Nh, Nh' \in M$,

\[ \underbrace{(Nh')(Nh)^{-1} \in M}_{\text{by the Subgroup Test}} \implies (Nh')(Nh^{-1}) \in M \implies N(h'h^{-1}) \in M. \]

However, in order for $N(h' h^{-1}) \in M$, we have that $h'h^{-1} \in H$. Since $h, h'$ were arbitrary elements of $H$, we have by the subgroup test we have that $H \le G$.

But since we have that $N \le G$, $H \le G$ and $N \subset H \subset G$, we all together have that $N \le H \le G$.

Next, we prove the the statements $(1)-(4).$ \textcolor{NavyBlue}{To prove (1), we'll show that $H/N \le K/N \implies H \le K$ and $H \le K \implies H/N \le K/N$ for any subgroups $H, K$ of $G$ which contain $N$ where $N \normal G$.}

\phantom{1} \hspace{0.5cm} Let $H, K$ be subgroups of $G$ such that $N \subset H$ and $N \subset K$. Furthermore, suppose that $H/N \le K/N$.

The Isomophism Theorems are extremely powerful. The following an application to something which matches our intuiton, but extremely difficult to prove without the isomophism theorems.

Let $G$ be a group and $H$ and $K$ be normal subgroups of $G$. Then

1. $HK$ is a subgroup of $G$
2. If $\gcd(|H|, |K|) = 1$ then $H \times K \cong HK$.

1. Observe that since $H \unlhd G$ and $K \unlhd G$, then obviously $H \le G$ and hence we can apply the Second Isomorphism Theorem to conclude that $HK \le G$. Thus we see that for this statement to be true in general we really only need one of the subgroups, either $H$ or $K$, to be normal to $G$.

\textcolor{NavyBlue}{To prove this, we'll construct an isomorphism between the two groups. In constructing the homomorphism, we'll have to do a bit of work to show our proposed homorphism is in fact a homomorphism, the work which lies in showing elements of $H$ and $K$ commute. Thus we will show this first.} * 2. The fact that $\gcd(|H|,|K|)=1$ allows us to concldue that neither $H \not \le K$ and $K \not \le H$, since otherwise by Lagrange's theorem the order of one group would divide the other, and obviously we don't have that case here. Thus we know that $H \cap K = \{e\}$, as by our previous argument it would be impossible for them to share any other nontrivial element. \ \ Since $H, K$ are normal to $G$ we'll have that

\[\begin{align*} hkh^{-1} \in K\\ kh^{-1}k^{-1} \in H \end{align*}\]

because $h$ and $k$ are both elements in $G$, and we know for all $a \in G$ that $aha^{-1} \in H$ for $h \in H$ and $aka^{-1} \in K$ for $k \in K$. We can then state that

\[\begin{align*} \overbrace{(hkh^{-1})}^{\text{A member of }K} \hspace{-0.3cm}k^{-1} = hkh^{-1}k^{-1} \in K\\ h\underbrace{(kh^{-1}k^{-1})}_{\text{A member of } H} = hkh^{-1}k^{-1} \in H \end{align*}\]

by using the fact that $H, K$ are subgroups and are therefore closed under products of their elements. But we showed earlier that $H \cap K = \{e\}$; hence $$ hkh^{-1}k^{-1} \in H \cap K = {e} \implies hkh^{-1}k^{-1} = e \implies hk = kh. $$ But $h, k$ were arbitrary elements of $H, K$, so this shows that products of their elements commute. \ \ Next, consider the function $\phi: H \times K \rightarrow HK$ defined as $$ \phi((h, k)) = hk. $$ which we will show to be a homomorphism. Observe that if $(h_1, k_1)$ and $(h_2, k_2)$ are in $H \times K$, then $$ \phi((h_1, k_1)\cdot(h_2, k_2)) = \phi((h_1h_2, k_1k_2)) = h_1h_2k_1k_2. $$ However, we showed that products of elements between $H$ and $K$ can commute, so that we can rewrite $h_2k_1$ as $k_1h_2$ to write $$ \phi((h_1, k_1)\cdot(h_2, k_2)) = h_1h_2k_1k_2 = h_1k_1h_2k_2 = \phi((h_1, k_2))\phi((h_2, k_2)). $$ Thus $\phi$ is a homomorphism. \ \ Observe now that $\text{ker}(\phi) = \{(e, e)\}$. This is because we know that $H \cap K = \{e\}$, so that if $$ \phi((h, k)) = hk = e $$ we know it is impossible that this could be because $h = k^{-1}$; otherwise, $H \cap K \ne \{e\}$, which we know is not the case. Hence the only time when $hk = e$ is if both $h$ and $k$ are $e$, so that $\text{ker}(\phi) = \{(e, e)\}$. \ \ Observe that $\text{im}(\phi) = HK$. This is because for any $hk \in HK$, we can simply observe that $h \in H, k \in K$, and therefore there exists a $(h, k) \in H \times K$ such that $$ \phi(h, k) = hk. $$ Thus every element of $HK$ is covered by our mapping, so $\phi$ is injective and hence $\text{im}(\phi) = HK$. \ \ Finally, what we have shown is that (1) $\phi$ is a homomorphism and (2) it is a bijection from $H \times K$ to $HK$. We can now apply the First Isomorphism Theorem to conclude that $$ H \times K/\text{ker}(\phi) \cong \text{im}(\phi) \implies H\times K \cong HK $$ because $\text{ker}(\phi) = \{(e, e)\}, H \times K/\{(e, e)\} = H \times K$, and $\text{im}(\phi) = HK$. This completes the proof.

The First Isomophism Theorem has a lot of fun applications, one of which we present here.

Let $G$ and $H$ be groups such that $|G|$ and $|H|$ are coprime. If $\phi: G \to H$ is a homomorphism, then $\phi$ is zero homomorphism.

By the First Isomorphism Theorem, we see that

\[ G/\ker(\phi) \cong \im(\phi). \]

Therefore $|G/\ker(\phi)| = |\im(\phi)|$. However,

\[\begin{align*} |G/\ker(\phi)| = |G|/|\ker(\phi)| &= |\im(\phi)|\\ \implies |G| &= |\ker(\phi)| \cdot |\im(\phi)|. \end{align*}\]

Note that $|\ker(\phi)| \mid |G|$ and $|\im(\phi)| \mid |H|$ by Lagrange's Theorem. However, we said that $|G|$ and $|H|$ are corpime which means that $|\im(\phi)| = 1$. Hence we must have that $|\ker(\phi)| = G$, and since $\ker(\phi) \le G$ we have that $\ker(\phi) = G$. Therefore $\phi$ sends every element of $G$ to the identity of $H$, which is what we set out to show.