2.8. Monoids, Groups and Groupoids in Categories
One of the most simplest, useful and yet underrated concepts in mathematics is the concept of a monoid. The reason why monoids are so useful is because they capture three main concepts: stacking "things" together to create another "thing," in such a way that our stacking operation is associative, with the additional assumption of an identity element which doesn't change the value. Often times in cooking up a mathematical construction, we want to maintain these three concepts because they are so familiar to our basic human nature.
Now recall the definition of a monoid.
A monoid \(M\) is a set equipped with a binary operation \(\cdot: M \times M \to M\) and an identity element \(e\) such that
- 1. For any \(x, y, z \in M\), we have that \(x \cdot (y \cdot z) = (x \cdot y) \cdot z\)
- 2. For any \(x \in M\), \(x \cdot e = x = e \cdot x\).
It turns out that we can abstract the above definition very easily if we just resist the temptation to explicitly refer to our elements. In order to do this, we need to find a way to diagrammatically express the above axioms.
Towards that goal, rename the binary operation as \(\mu: M \times M \to M\) (for notational convenience).
Then to express axiom
(1), we mean that we have 3 elements \(x, y, z \in M\) and there are two ways to compute them, but we
want them to be the same. So lets make each different way to compute them one side of a square, which
we'll say it commutes.
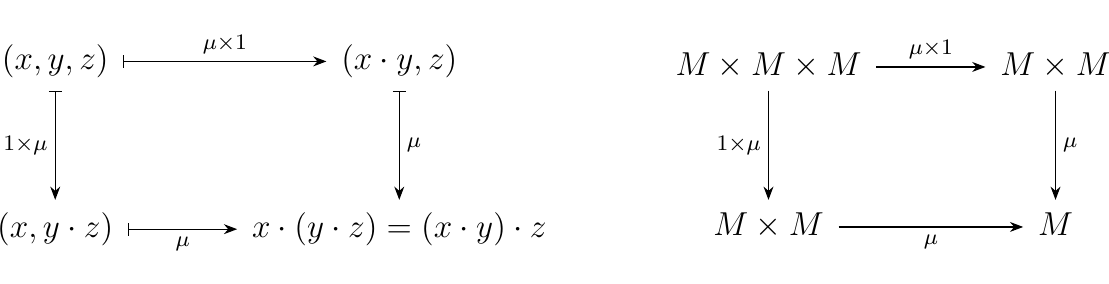 The result is the diagram on the above left. Since we want this to hold for
all elements in \(M\), we construct the diagram more generally on the above right;
this expresses our associativity axiom. Now to express the second axiom diagrammatically, we need a way to discuss the
identity map. So define the map \(\eta: \{\bullet\} \to M\) where \(\eta(\bullet) = e\). This
is just a stupid map that picks out the identity. Then axiom (2) can be translated
diagramatically to state that the bottom left diagram commutes.
The result is the diagram on the above left. Since we want this to hold for
all elements in \(M\), we construct the diagram more generally on the above right;
this expresses our associativity axiom. Now to express the second axiom diagrammatically, we need a way to discuss the
identity map. So define the map \(\eta: \{\bullet\} \to M\) where \(\eta(\bullet) = e\). This
is just a stupid map that picks out the identity. Then axiom (2) can be translated
diagramatically to state that the bottom left diagram commutes.
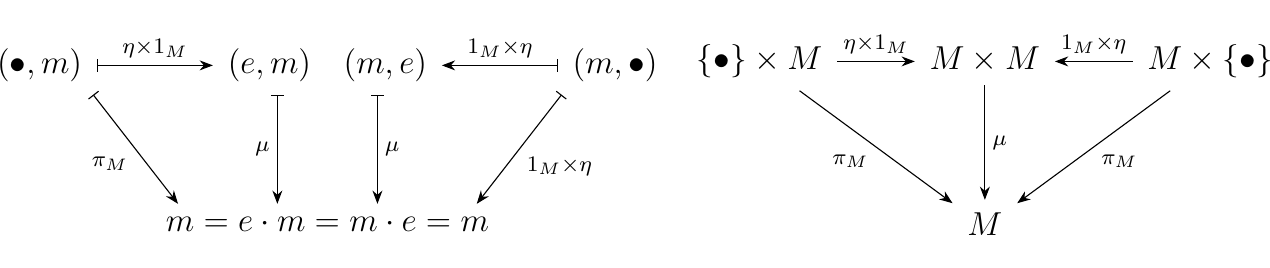 Since we want this to hold for all \(m \in M\), we generalize this to create a
commutative diagram as on the above right. We now have what we need to define a monoid more generally.
Since we want this to hold for all \(m \in M\), we generalize this to create a
commutative diagram as on the above right. We now have what we need to define a monoid more generally.
Let \(\cc\) be a category with cartesian products. Denote the terminal object as \(T\). An object \(M\) is said to be a monoid in \(\cc\) if there exist maps
such that the diagrams below commute.
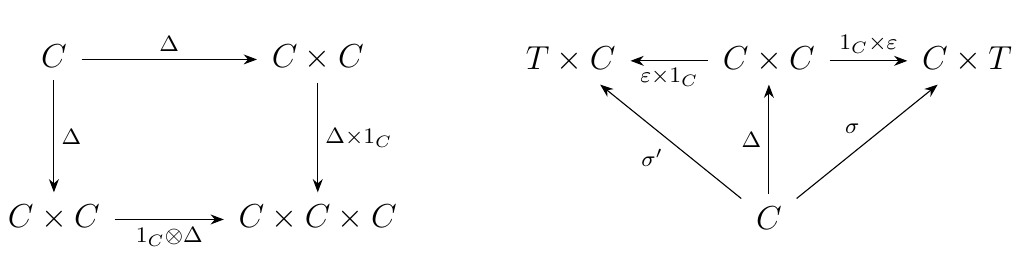
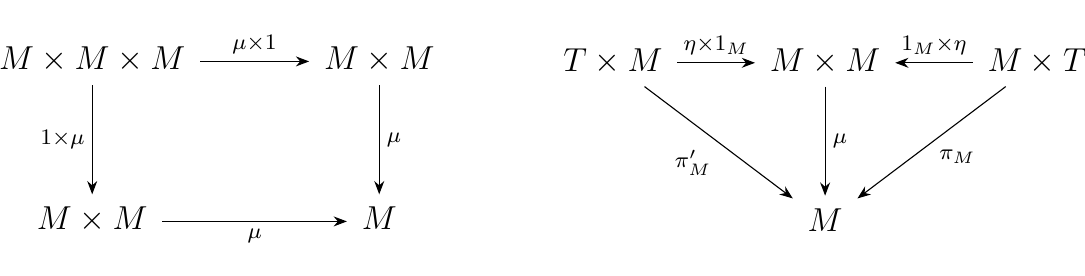 Dually, a comonoid is an object \(C\) with maps
Dually, a comonoid is an object \(C\) with maps
such that the dual diagrams commute.
 \textcolor{NavyBlue}{Note that we're being a little sloppy here. For example, the object
\(M \times M \times M\) doesn't actually exist; we have either \(M \times (M \times M)\) or \((M \times M) \times M\).
} However, for any category with cartesian products, we always have that these two objects
are isomorphic. Hence we mean either of the equivalent products when we discuss \(M \times M \times M\).
\textcolor{NavyBlue}{Note that we're being a little sloppy here. For example, the object
\(M \times M \times M\) doesn't actually exist; we have either \(M \times (M \times M)\) or \((M \times M) \times M\).
} However, for any category with cartesian products, we always have that these two objects
are isomorphic. Hence we mean either of the equivalent products when we discuss \(M \times M \times M\).
Let \(k\) be a field. Consider the category \(**Vect**_k\). Then a monoid in this category is an object \(A\) equipped with maps
Group object in the category of Top is a topological group.
Monoid in the category of \(R\) modules is an associative algebra.
\chapterimage{chapter3_pic/chapt3head.pdf}