11.2. Generalized Persistence Modules.

Let \(P\) be a preorder. Then a generalized persistence module is a functor \(F: P \to \dd\). Therefore, we may view \(D^P\) to be the category of generalized persistence modules on \(P\).

A translation on \(P\) is a functor \(\Gamma: P \to P\) such that \(x \le \Gamma(x)\) for all \(x\). Equivalently, it is any functor such that there exists a natural transformation \(\eta_\Gamma: I \to \Gamma\).

We can denote the category of translations on \(P\) as \(**Trans**_P\). Note that this is a preorder. Since \(P\) is a preorder, any two natural transformations between two functors must necessarily be equal. Moreover, every pair of translations must have a natural transformation; that is, one (or both) of the diagrams below must commute for any \(x \le y\) in \(P\).

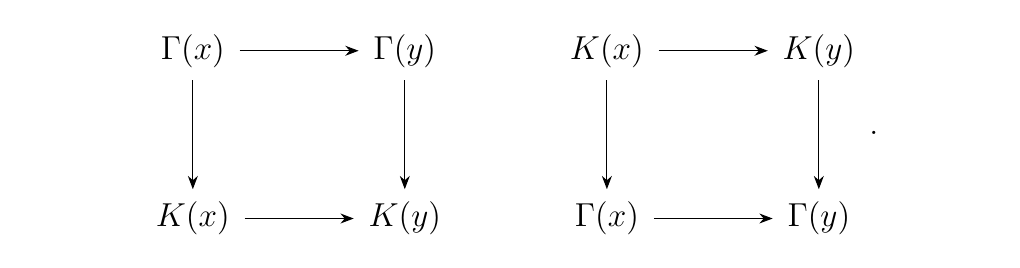Thus we set \(\Gamma \le K\) whenever there exists a natural transformation \(\eta_{\Gamma K}: \Gamma \to K\).

Let \(P\) be a preorder and \(\Gamma, K \in **Trans**_P\). Suppose \(F, G \in \dd^P\). We say \(F, G\) are \((\Gamma, K)\)-interleaved if there exists a pair of natural transformations \(\phi: F \to G \circ \Gamma\) and \(\psi: G \to F\circ K\) such that

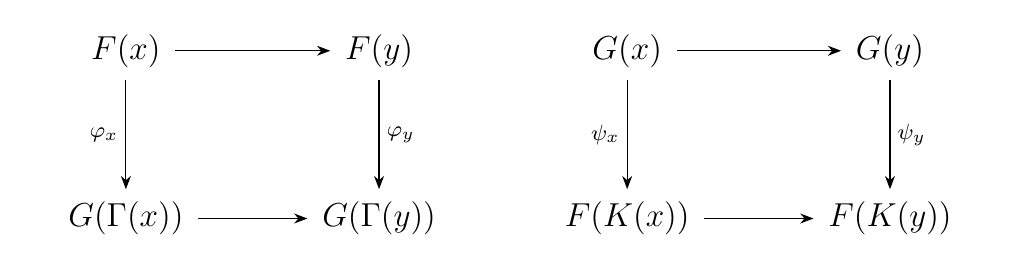
Note that, given the first two commutative squares, we can stack them to create a larger commutative square:

If the two triangular diagrams did not hold, then we would we would see that there would be two different, but not necessarily equal ways of getting from \(F\) to \(F(K(\Gamma))\) and \(G\) to \(G(\Gamma(K(x)))\). Note also that, if we really wanted to, we could keep stacking these diagrams on and on.

The interleaving of two functors satisfies the following three properties.

[Functoriality] Let \(\Gamma, K\) be translations on a preordered set \(P\). If \(F, G \in \dd^P\),
and if \(F, G\) are \((\Gamma, K)\)-interleaved, then \(H\circ F\) and \(H \circ G\) are also \((\Gamma, K)\) interleaved.

This is true since any functor applied to a commutative diagram will output a commutative diagram. Thus if we compose \(H\) with the commutative diagrams which arise from the interleaving of \(F, G\), we get

The above diagrams can be reconciled with the definition of an \((\Gamma, K)\) interleaving, so that \(H\circ F, H\circ G\) are \((\Gamma, K)\) are
interleaved.

[Monotonicity] Let \(\Gamma_1, \Gamma_2, K_1, K_2\) be translations of a preordered set \(P\) such that \(\Gamma_1 \le \Gamma_2\) and \(K_1 \le K_2\). If two persistence modules \(F, G \in \dd^{P}\) are \((\Gamma_1, K_1)\) interleaved, then they are also \((\Gamma_2, K_2)\) interleaved.

Since \(\Gamma_1 \le \Gamma_2\) and \(K_1 \le K_2\), there must exist natural transformations \(\alpha: \Gamma_1 \to \Gamma_2\) and \(\beta: K_1 \to K_2\). Now since \(F, G\) are \((\Gamma_1, K_1)\)-interleaved, this means we get the usual diagrams, but we can stack an extra layer on the bottom.

Hence we can see our natural transformations of interest are \(G(\alpha) \circ \phi: F \to G \circ \Gamma_2\) and \(F(\beta)\circ \psi: G \to F \circ K_2\). We now have to show that our two required triangular diagrams must commute. Towards this goal, consider the diagram below.

The left triangle commutes since \(F, G\) are a \((\Gamma_1, K_1)\) interleaving, while the rightmost commutes by the original square diagrams. We've outlined their correspondence in colors. We almost have what we want, but we need to make sure \(\textcolor{Orange}{F(K_2(\alpha_x))}\circ \textcolor{Blue}{F(\beta_{\Gamma_1(x)})}\circ F(\eta_{\Gamma_1(K_1(x))}) = F(\eta_{\Gamma_2(K_2(x))})\). To do this, observe that the diagram

must necessarily commute as it is a diagram inside of \(P\), a preordered set. Therefore, the image of this diagram under \(F\) must produce a commutative diagram, so that we do in fact get our desired relation. All together, we then have

The same procedure can be repeated dually to demonstrate commutativity for the other required triangular diagram. Thus we have that \(F, G\) are \((\Gamma_2, K_2)\)-interleaved.

[Triangle inequality.] Let \(\Gamma_1, \Gamma_2, K_1, K_2\) be translations of a preordered set \(P\). Suppose \(F, G, H \in \dd^P\). Then if \(F,G\) are \((\Gamma_1, K_1)\)-interleaved and \(G, H\) are \((\Gamma_2, K_2)\)-interleaved, then \(F,H\) are \((\Gamma_2\circ\Gamma_1, K_1\circ K_2)\)-interleaved.

First observe that since \(F, G\) are \((\Gamma_1, K_1)\)-interleaved and \(G,H\) are \((\Gamma_2, K_2)\)-interleaved, we have the natural transformations

\[\begin{align*} \phi&: F \to G \circ \Gamma_1 &&\phi': G \to H\circ \Gamma_2\\ \psi&: G \to F\circ K_1 &&\psi': H \to G\circ K_2 \end{align*}\]

which satisfy the required diagrams. Consider the diagrams

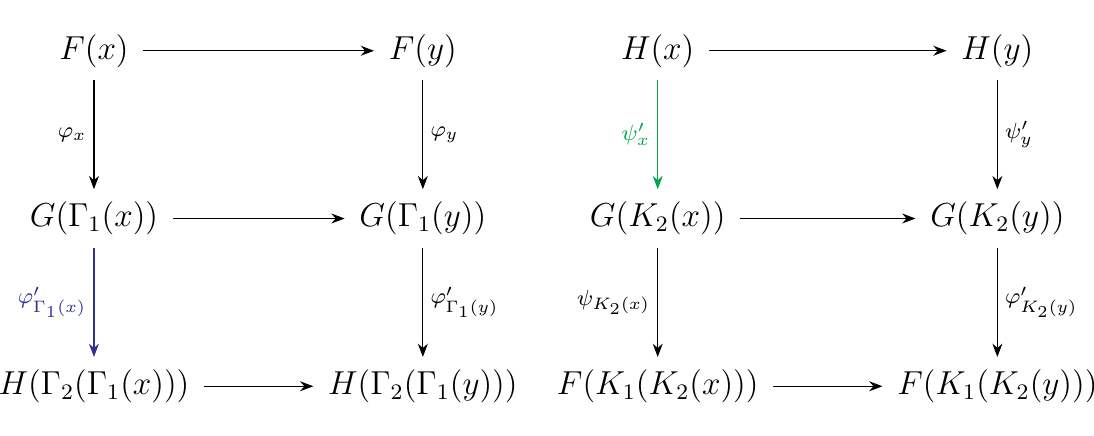which commute by our given interleavings. Then there are natural transformations \(\psi'_{\Gamma_1} \circ \phi: F \to H(\Gamma_2\circ\Gamma_1)\) and \(\phi'_{K_2}\circ \psi: H \to F(K_1\circ K_2)\). We now must check they satisfy the required triangular diagrams. We can demonstrate this for at least one; Consider the diagram

The above diagram commutes by our given interleavings. The diagram in \textcolor{Blue}{blue} commutes since \(F, G\) are \((\Gamma_1, K_1)\) interleaved, while the diagram in \textcolor{Red}{red} commutes since \(G, H\) are \((\Gamma_2, K_2)\)-interleaved.