7.8. Enriched Categories

When we originally defined categories, we sought a degree of large generality that was able to capture a huge amount of mathematical phenomenon. However, this was not out a mere desired for generality; as Mac Lane puts it, "good general theory does not search for the maximum generality, but for the right generality" (108). But it does turn out that in defining categories so widely we lose some of their internal structure; for example, in many categories, every homset might have a underlying abelian group structure. These are called preadditive categories and are extremely useful, in that they give us a first step towards a general framework (but not to general) that allows one to do homological algebra in.

Now if we've lost some original framework, how do we recover it? First, recall that in categories, objects are basically dummies. It doesn't matter how I denote my objects in my category $\cc$; you and are I talking about the same category if our morphisms act the same exact way. For example, the categories

and

where the above objects are $n$ words describing how politicians suck, are the same preorders. Thus, because categorical structure is primarily found within the morphisms, i.e. the homsets, we only need to fix these to take back our original structure.

Let $(\mathcal{V}, \otimes, I)$ be a monoidal category. A small category $\cc$ is a $\mathcal{V}$-category or an enriched category over $\mathcal{V}$ if

1. For each $A, B \in \cc$, we have that $\hom_{\cc}(A, B) \in \mathcal{V}$
2. There exists a "composition" operator

$$ \circ_{A, B, C} : \hom_{\cc}(A, B) \times \hom_{\cc}(B, C) \to \hom_{\cc}(A, C) $$ * 3. For each object $A \in \cc$, we have a "identity object"

\[ i_A: I \to \hom_{\cc}(A, A) \]

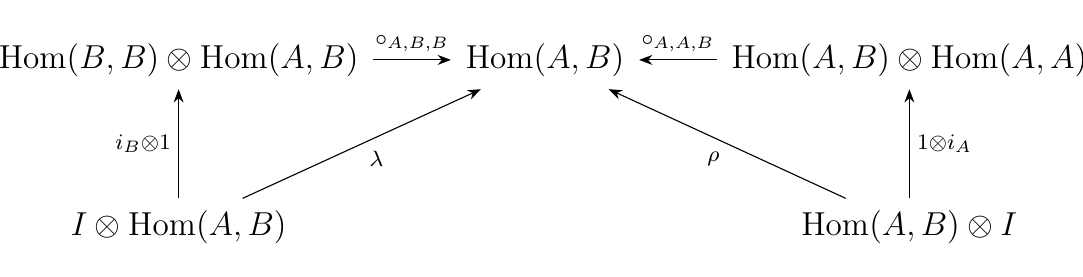
such that our composition operator is associative:

and such that our unital elements in each homset behave morally like an identity element should:

The following is a classic example due to F.W. Lawvere. A Lawvere metric space is a set $X$ equipped with a distance function $d: X\times X \to \rr$ such that

1. $d(x, x) = 0$ for all $x \in X$
2. $d(x, z) \le d(x, y) + d(y, z)$ for all $x, y, z \in X$.

It turns out that, we may equivalently define such a space as a category enriched over $([0, \infty), +, 0)$.

Recall that $([0, \infty), +, 0)$ where $+$ is addition forms a symmetric monoidal category. Here we treat $[0, \infty]$ as a poset where for a pair of objects $a, b$ there exists exactly one morphism

\[ a \to b \text{ iff } b \le a. \]

Now what does it look like for a category $\cc$ to be $[0, \infty]$-category? It means that for any pair of objects $A, B$, we have that $\hom_{\cc}(A, B) \in [0, \infty)$. If we denote $d(A, B) = \hom_{\cc}(A, B)$, this then implies that we have a function

\[ d: \ob(\cc)\times\ob(\cc) \to [0, \infty]. \]

Enriched categories also grant us a composition morphism

\[ \hom_{\cc}(A, B) \times \hom_{\cc}(B, C) \to \hom_{\cc}(A, C) \]

for all objects $A, B, C$. But in $[0, \infty)$, morphisms are just size relations, so what this really means is that

\[ d(A,C) \le d(A, B) + d(B, C) \]

for all $A, B, C \in \cc$ Finally, we see the identity criterion states that for each object $A$, we have a morphism $i_{A}: 0 \to \hom_{\cc}(A, A)$ which translates to

\[ d(A, A) \le 0 \implies d(A, A) = 0 \]

since $d(A, A) \in [0, \infty]$. This should feel very familiar; what we've just come up with is nearly a metric space structure on the objects of our category! We are only missing the symmetry relation. For that, this special construction is known as a Lawvere metric space.

Recall that a (strict) 2-category is a category $\cc$ such that, in addition to the morphisms $f: A \to B$ between objects $A, B \in \cc$, there exists 2-morphisms $\alpha: f \to g$ between parallel morphisms $f, g: A \to B$.

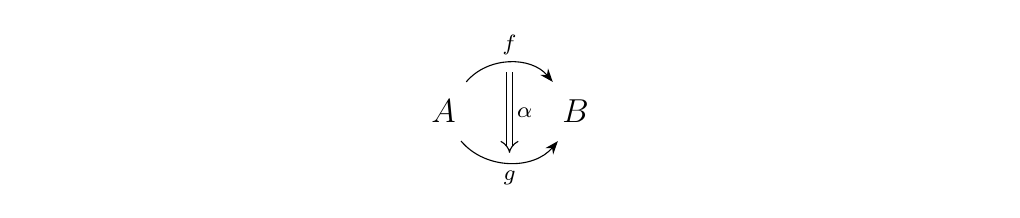These two morphisms have access to two different forms of composition. On one hand, there is "vertical" composition

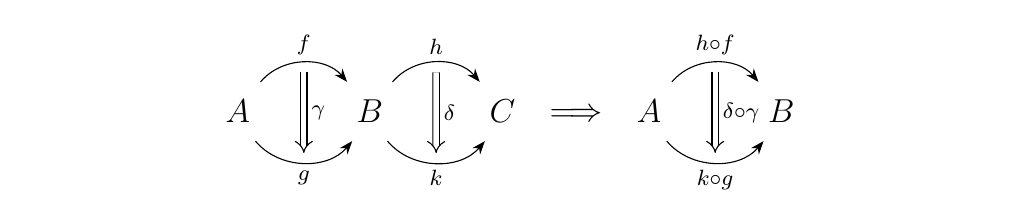
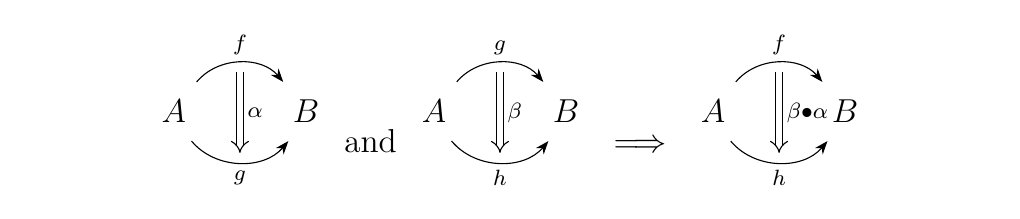while on the other, there is "horizontal" composition.

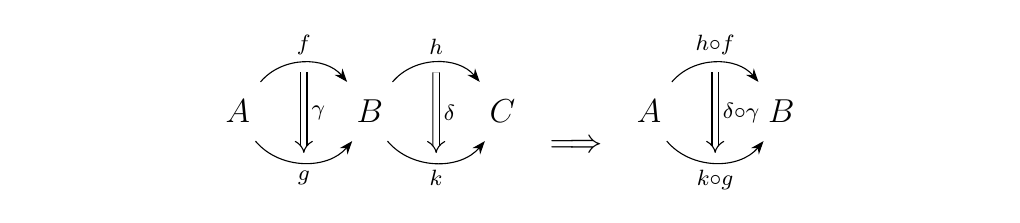Moreover, we require that the interchange law be satisfied and that the morphisms form a category under the vertical composition given by $\circ$. However, we can rephrase this as saying a category $\cc$ is a 2-category if

1. For each $A, B \in \cc$ we have that $(\hom_{\cc}(A, B), \circ)$ is a category
2. There exist a composition operator $\circ : \hom(A, B) \times \hom(B, C) \to \hom(A, C)$

* 3. For each object $A$, we have a functor $i_A: 1 \to \hom(A, A)$, where $1$ is the one object category with one morphism that is sent to $1_A$.

Above, (3) is stupidly simple; but the reason we're framing it this way is to demonstrate that a strict 2-category $\cc$ is the same thing as a category $\cc$ enriched over the monoidal category $(**Cat**, \times, 1)$; the category of small categories whose monoidal product is the cartesian product and whose identity is the one-object-one-morphism category $1$.