11.1. Persistence modules on \(\rr\).

Let \(\cc\) be a category, and denote \((\rr, \le)\) to be the poset category on \(\rr\) with respect to the natural relation \(\le\). We define a functor \(F: (\rr, \le) \to \cc\) to be a persistence module.

Thus we can say that a persistence module is an element of the functor category \(\cc^{\rr}\).

A persistence module allows us to model the evolution of objects within some category \(\cc\). For example, if we have some ascending chain of vector spaces

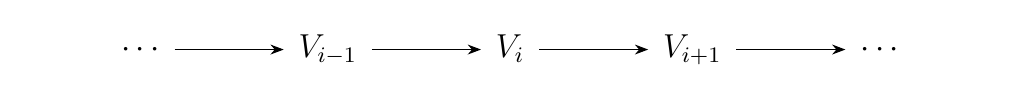then we say that such a chain is a persistence module since it can be modeled as a functor from \(\rr \to **Vec**\).

Let \(S = \{s_1, s_2, \dots, s_n\}\) be a finite subset of \(\rr^n\). Then we can describe
an adjunction

as follows. First observe that since \(S \subset \rr\), there exists a restriction functor \(R: \cc^{\rr} \to \cc^{S}\), which acts as a restriction (hence the naming \(R\)):

\[ R(F: \rr \to \cc) = F\big|_{S}: S \to \cc. \]

How can we write a functor going in the opposite direction? That is, given a persistence module which acts on \(S\),

is there a canonical way to extend this to a persistence module which acts on the rest of \(\rr\)?

One way we may extend a persistence module \(K: S \to \cc\) in \(\cc^S\) to a persistence module in \(\cc^{\rr}\) is to define a functor \(\overline{K}: \rr \to \cc\) where

\[ \overline{K}(r) = \begin{cases} I & \text{if } s < s_1\\ K(r) & \text{if } s_{i} \le r \le s_{i+1}\\ K(r_n) & \text{if } r > s_n \end{cases} = \begin{cases} I & \text{if } r < \text{min}(S)\\ K(s_r) & \text{where } s_r \text{ is the largest } s_r \in \text{ S such that } s_r \le r. \end{cases} \]

Now consider a morphism \(\eta: K \to P\) in \(\cc^{S}\); that is, a natural transformation. By our above procedure we have a way of discussing the objects \(\overline{K}\) and \(\overline{P}\); but can we obtain a natural transformation \(\overline{\eta}: \overline{K} \to \overline{P}\) from \(\eta\)? That is, may we extend this relationship to a functor?

First, observe that we may write \(\eta: K \to P\) as follows.

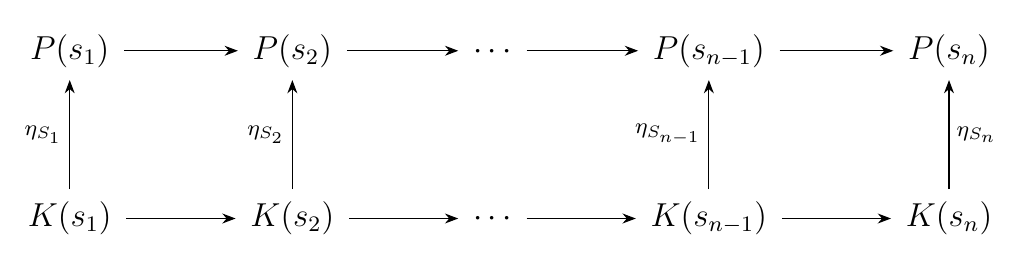The top and bottom rows come about by functoriality of \(K\) and \(P\),
while the upward arrows are the family of morphisms created by the existence of a natural transformation.

We can extend this to a natural transformation \(\overline{\eta}: \overline{K} \to \overline{P}\) by stating

\[ \overline{\eta}_r = \begin{cases} 1_I & \text{if } r < s_1 \text{, where } I \text{ is initial}\\ \eta_{s_r} & \text{where } s_r \text{ is the largest } s_r \in S \text{ such that } s_r \le r. \end{cases} \]

\subsection*{Adjoint Functors}

Thus we see that we really do have a functor \(\cc^{S} \to \cc^{\rr}\) on our hands If we denote this as a functor \(E: \cc^{S} \to \cc^{\rr}\), where \(E\) can be read as extends, then we overall have

We can now demonstrate that this pair of functors gives rise to an adjunction; there a few ways to do this. We'll demonstrate that

\[ \hom_{\cc^{S}}(K, P_S) \cong \hom_{\cc^{\rr}}(\overline{K}, P) \]

is natural, where \(P_S = \text{R}(P)\) and \(\overline{K} = E(K)\). Towards this goal, consider a morphism \(\eta: K \to P_S\). Then we have something like this again

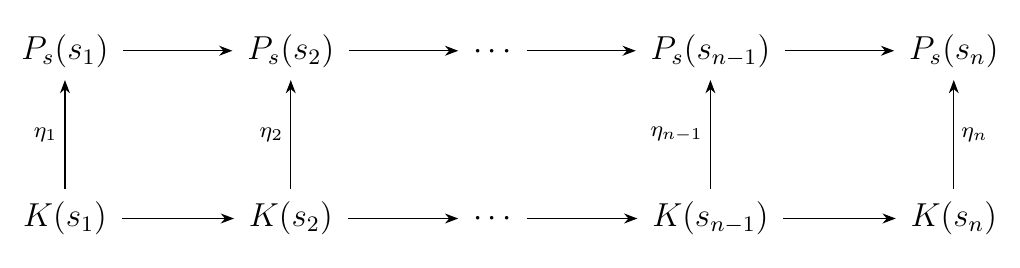Now we seek a natural transformation \(\eta': \overline{K} \to P\). Since \(\overline{K}\) is constructed from \(K\), a good choice would be to write \(\eta'_{s_i} = \eta_{s_i}\) for \(s_i \in S\). Now our concern is considering how to define \(\eta'_r\) when \(r \not \in S\). That is, we want something like

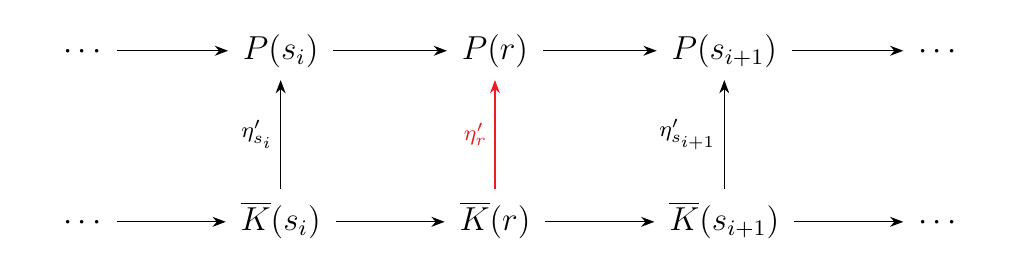To define the morphism in red, we first recall that in this situation we have \(K(r) = K(s_i)\). Hence we know that any morphism
from \(K(r)\) must originate from \(K(s_i)\); one such morphism we already know about is \(\eta_{s_i}: K(s_i) \to P_s(s_i)\). Now, \(P_s(s_i) = P(s_i)\); and in our case the desired target for \(\eta'\) is \(P(r)\), not \(P(s_i)\). However, we can compose this with the morphism \(P(j): P(s_i) \to P(r)\). where \(j : s_i \to r\).

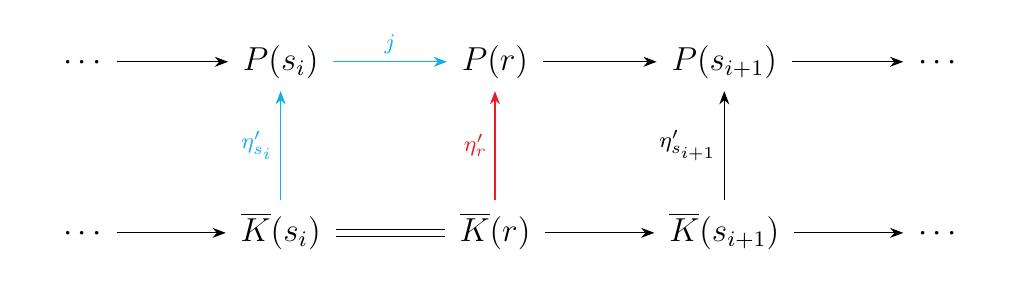Therefore, in this case we define

\[ \eta'_{r} := P(j) \circ \eta_{s_i}. \]

which necessarily forces commutativity, and hence demonstrating naturality of \(\eta'\). Now what if \(r < s_1\) or \(s_n < s\)? In the first case, \(K(r) = I\), and \(\eta'_r\) becomes the unique morphism from \(I \to P(r)\). \textcolor{NavyBlue}{This presents one benefit of adding the criteria \(K(r) = I\) if \(r < s_1\)}. By uniqueness of this morphism we get a commutative square. In the second case, we proceed as above. Therefore

\[ \eta'_r = \begin{cases} i_{P(r)}: I \to P(r) & \text{if } r < s_1\\ P(j: s_i \to r) \circ \eta_{s_i} & \text{where } s_i \text{ is the largest } s \in S \text{ such that } s \le r. \end{cases} \]

Therefore, we can define a map \(\textcolor{Blue}{\phi}: \hom_{\cc^S}(K,P_S) \to \hom_{\cc^{\rr}}(\overline{K}, P)\) where

\[ \phi(\eta: K \to P_S) = \eta': \overline{K} \to P. \]

Consider the map \(\psi: \hom_{\cc^{\rr}}(\overline{K}, P) \to \hom_{\cc^S}(K, P_S)\) where

\[ \psi(\sigma: \overline{K} \to P) = \sigma': K \to P_S \]

where we set \(\sigma'_s = \sigma_s\). While this map is particularly boring, we're discussing it because we can now see that \(\psi\) and \(\phi\) are inverses of each other. Therefore, we see that we have a bijection between the hom-sets, as desired.

\subsection*{Naturality.}

Finally, we must demonstrate naturality. So suppose we have a natural transformation \(\alpha: K \to K'\) between two persistence modules \(K, K' : S \to \cc\). Consider the squares below, which we do not yet know commutes.

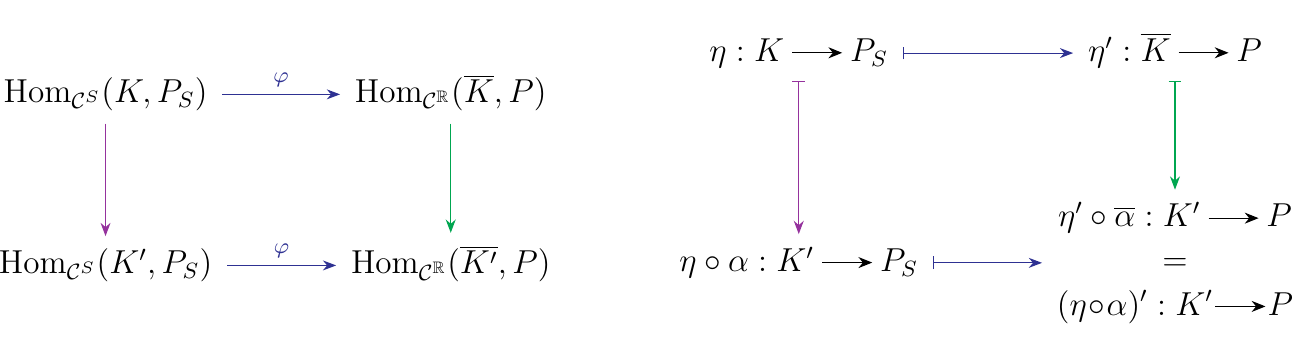
Note that on one hand,

\[ \overline{\alpha}_r = \begin{cases} 1_I & \text{if } r < s_1 \text{, where } I \text{ is initial}\\ \alpha_{s_r} & \text{where } s_r \text{ is the largest } s_r \in S \text{ such that } s_r \le r. \end{cases} \]

and

\[ \eta'_r = \begin{cases} i_{P(r)}: I \to P(r) & \text{if } r < s_1\\ P(j: s_i \to r) \circ \eta_{s_i} & \text{where } s_i \text{ is the largest } s \in S \text{ such that } s \le r. \end{cases} \]

so that

\[\begin{align*} (\eta' \circ \overline{\alpha})_r &= \begin{cases} i_{P(r)}: I \to P(r) & \text{if } r < s_1\\ \big(P(j: s_i \to r ) \circ \eta \big)\circ\alpha & \text{where } s_r \text{ is the largest } s_r \in S \text{ such that } s_r \le r. \end{cases}\\ &= \begin{cases} i_{P(r)}: I \to P(r) & \text{if } r < s_1\\ P(j: s_i \to r ) \circ (\eta \circ\alpha) & \text{where } s_r \text{ is the largest } s_r \in S \text{ such that } s_r \le r. \end{cases}\\ &= (\eta \circ \alpha)'_r. \end{align*}\]

Since we know that \(\big(P(j: s_i \to r)\circ \eta \big)\circ\alpha = P(j: s_i \to r) \circ (\eta \circ \alpha)\). Thus we see that the previous squares we discussed do in fact commute.

Now suppose we have a natural transformation \(\sigma: P \to P'\) between two functors \(P, P': \rr \to \cc\). Consider the diagrams below, which we will show are commutative.

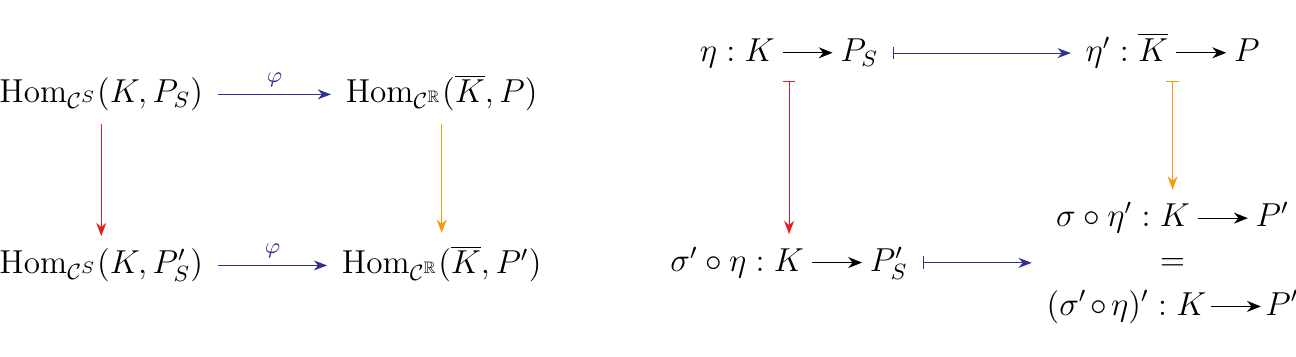To show this, observe that

\[\begin{align*} \sigma \circ \eta' &= \begin{cases} \sigma_r \circ i_{P(r)}: I \to P'(r) & \text{if } r < s_1\\ \sigma_{r}\circ P(j: s_i \to r) \circ \eta_{s_i} & \text{where } s_i \text{ is the largest } s \in S \text{ such that } s \le r. \end{cases}\\ &= \begin{cases} \textcolor{Purple}{i_{P'(r)}: I \to P'(r)} & \text{if } r < s_1\\ \textcolor{OliveGreen}{P'(j: s_i \to r)} \circ (\sigma \circ \eta )_{s_i} & \text{where } s_i \text{ is the largest } s \in S \text{ such that } s \le r. \end{cases}\\ &= \begin{cases} i_{P'(r)}: I \to P'(r) & \text{if } r < s_1\\ P'(j: s_i \to r) \circ (\textcolor{Red}{\sigma'} \circ \eta )_{s_i} & \text{where } s_i \text{ is the largest } s \in S \text{ such that } s \le r. \end{cases}\\ &= (\sigma' \circ \eta)'. \end{align*}\]

The diagrams below can assist to seeing why this is the case. First, the change in \textcolor{Purple}{purple} occurs by commutativity of the diagram on the left; the commutativity results due to the universal nature of morphisms originating from the initial object \(I\). Second, the changes in \textcolor{OliveGreen}{green} and \textcolor{Red}{red} occur by commutativity of the diagram on the right.

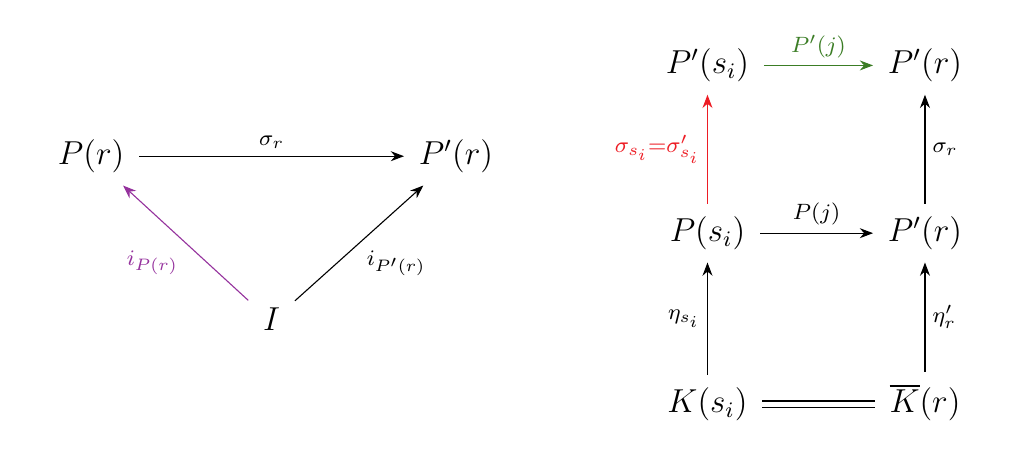Thus we see that our original squares are commutative. At this point, we can conclude that we do in fact have an adjunction

as desired.