Skip to content

3.7. Equalizers and Coequalizers

We introduce equalizers and coequalizers as further examples of limits, and therefore examples of universal morphisms. Equalizers and coequalizers are important constructions that are useful for proofs and definitions that we will encounter later on. We first introduce examples of equalizers and coequalizers.

Let \(G\) and \(H\) be groups, and consider a pair of homomorphisms \(\phi\) and \(\psi\) as below.

Now consider the homomorphism \(\phi - \psi:G \to H\). Then observe that

\[ \ker(\phi - \psi) = \bigg\{ g \in G \;\bigg|\; (\phi - \psi)(g) = 0 \bigg\} \]

and note that this is also the set of all \(g \in G\) in which \(\phi\) and \(\psi\) agree. In fact, it is the smallest such set, a notion we can make precise by the following observation: If \(G'\) is another group with \(\vartheta: G' \to G\) another map such that \(\phi \circ \vartheta = \psi \circ \vartheta\), then there exists a unique \(i: G' \to \ker(\phi - \psi)\) such that the diagram below commutes.

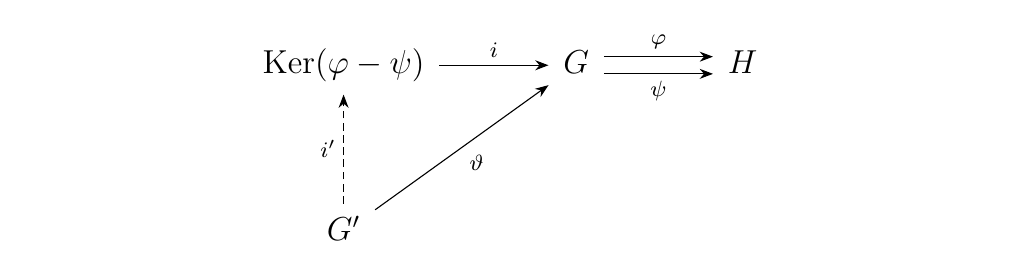Note above that \(i: \ker(\phi - \psi) \to G\) is the inclusion morphism. Also note that this construction is possible for any two parallel group homomorphisms.

In Set, equalizers always exist. Simply let \(D = \{x \in A \mid f(x) = g(x)\}\), and let \(e: D \to A\) by the inclusion morphism into \(A\). Clearly we'll have that \(f \circ e = g \circ e\).

Now for any \(h: C \to A\) such that \(f \circ h = g \circ h\), we see that the image of \(h\) must be a subset of \(D\). Hence there exists a unique inclusion morphism \(i: C \to D\), which shows that \(e\) in fact is the equalizer in Set for any \(f, g: A \to B\).

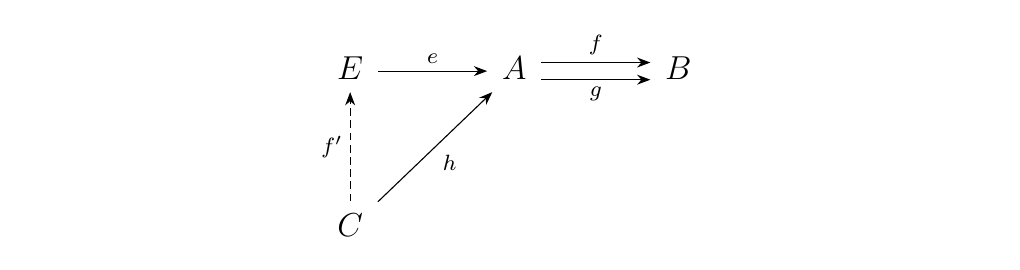
[Nice Equalizer Definition] Let \(\cc\) be a category and consider a pair of parallel morphisms \(f, g: A \to B\). The equalizer of \(f\) and \(g\) is a pair \((E, e: E \to A)\) such that \(f \circ e = g \circ e\) with the following property. For any other morphism \(h: C \to A\) such that \(f \circ h = g \circ h\), there exists a unique morphism \(f': C \to E\) such that the following commutes.

[Equalizer as a Limit] Let \(\cc\) be a category and consider a pair of parallel morphisms \(f, g: A \to B\). Let \(J\) be the category with two elements and two nontrivial morphisms as below.

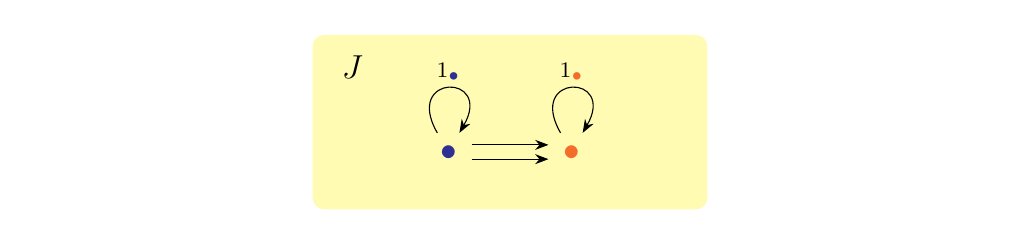
and let \(F: J \to \cc\) be the functor such that

\(=\)

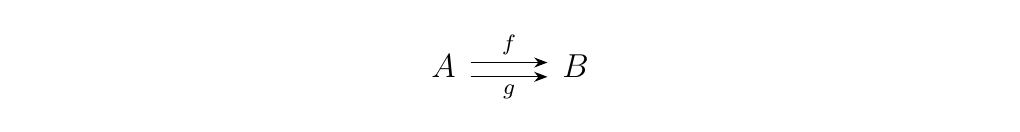
We define the equalizer of \(f\) and \(g\) to be limit \((\Lim F, e: \Delta(\Lim F) \to F)\) of \(F\).

Let \(\cc\) be a category, and suppose \(e: D \to A\) is an equalizer for a pair of morphisms \(f, g: A \to B\). Then \(e\) is monic.

Consider any pair \(f_1, f_2: C \to D\) such that \(e \circ f_1 = e \circ f_2\). Then we have that

Since \(e \circ f_1 = e \circ f_2\), we see that

\[\begin{align*} f \circ e = g \circ e &\implies f \circ (e \circ f_1) = g \circ (e \circ f_1)\\ &\implies f \circ (e \circ f_1) = g \circ (e \circ f_2). \end{align*}\]

Hence we see \(e \circ f_1 = e \circ f_2 : C \to D\) is another morphism which is equalized by \(f\) and \(g\).

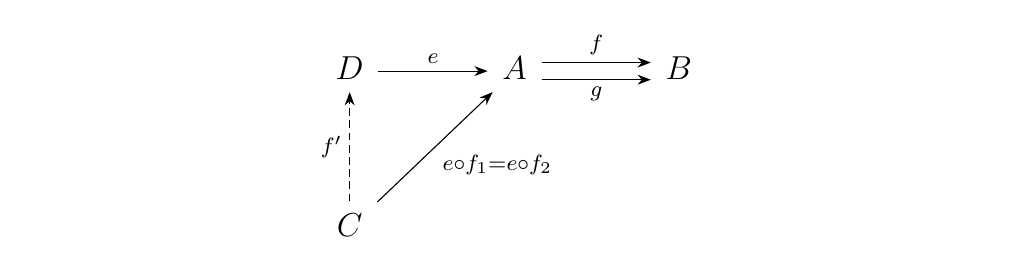By the universality of the equalizer \(e: D \to A\), we know that there must exist a unique morphism \(f': C \to D\) such that

\[ e \circ f' = e \circ f_1 = e \circ f_2. \]

Since \(f'\) is unique, we are forced to conclude that \(f_1 = f_2\). Hence \(e \circ f_1 = e \circ f_2 \implies f_1 = f_2\), so that \(e: D \to A\) is monic.

Let \(\cc\) be a category with a zero object \(Z\) of \(\cc\). That is, an object which is both initial and terminal, such that for any objects \(A, B\) of \(\cc\) there exists a unique pair of morphisms \(f, g\) such that

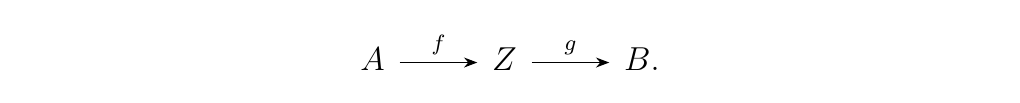Denote \(f \circ g = 0\) as the zero arrow (any morphism which passes through \(z\) is a zero arrow).

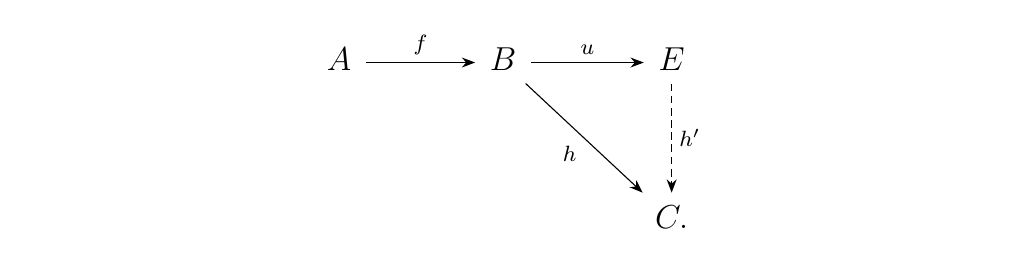
Now we define the cokernel a morphism \(f: A \to B\) to be an arrow \(u:B \to C\) where

  • 1. \(u \circ f = 0: A \to C\)
  • 2. If \(h: B \to D\) has the property that \(h \circ f = 0\), then \(h = h' \circ u\) for a unique arrow \(h': B \to D\).

Visually, this becomes


The cokernel is a special object in Ab, as it plays a role in the concept of exact sequences and hence homology as well. The cokernel of a homomorphism \(f: G \to H\) is the projection \(H \to H/\im(G)\), a quotient group of \(B\). This is often written as

\[ \text{coker}(f) = H/\im(G). \]

\subsection*{\underline{Coequalizers.}}

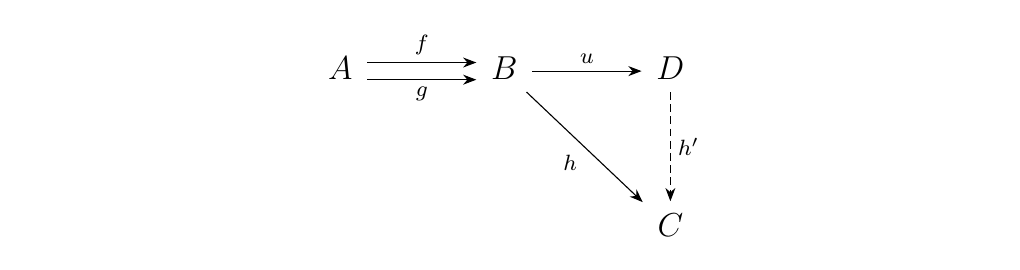
Let \(\cc\) be a category and consider two morphisms \(f, g: A \to B\) in \(\cc\). The coequalizer of \((f, g)\) is a morphism \(u: B \to D\) such that

  • 1. \(u \circ f = u \circ h\)
  • 2. If \(h: B \to C\) has the property that \(h \circ f = h \circ g\), then there exists a unique morphism \(h':D \to C\) such that \(h = h' \circ u\).

This may not always exist. We can represent this with the following commutative diagram.\ \textcolor{NavyBlue}{Note that we can interpret a coequalizers as a morphism which uniquely "flattens" morphisms, and for any other morphism which also "flattens" is related to the original coequalizer.}

With coequalizers, we get the following nice result.

All coequalizers are epimorphisms.

Coequalizers can also be realized as universal arrows. First consider the category 2, containing two objects and two nontrivial morphisms. Since there are only two objects, the two nontrivial morphisms have the same domain and codomain. Now consider the functor category \(\cc^**2**\) where

  • 1. Objects are functors \(F: **2** \to \cc\), whose image is therefore a pair of morphism \(f, g: A \to B\) in \(\cc\)
  • 2. Morphisms are natural transformations, which are therefore a pair of arrows \(h : A \to A'\) and \(k: B \to B'\) so that

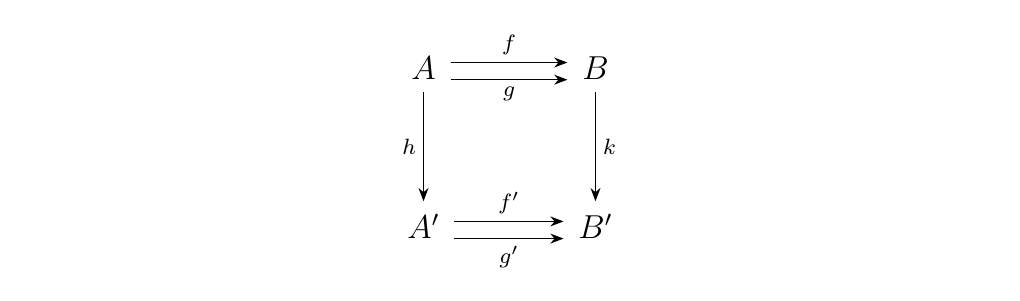is a commutative diagram. Finally consider the diagonal functor \(\Delta: \cc \to \cc^**2**\) where

\[\begin{align*} C &\longmapsto (1_C, 1_C)\\ r: C \to C' &\longmapsto (r, r). \end{align*}\]

Now consider a pair \(f, g: A \to B\) in \(\cc^{**2**}\). If we have a morphism \(h: B \to C\) such that \(h\circ f = h \circ g\), then this is the same thing as a morphism \((hf, hg): (f, g) \to (1_C, 1_C)\) in \(\cc^{**2**}\). Therefore a coequalizer \(u: B \to C\) is a universal arrow from \((f, g)\) to \(\Delta\).

In the category Ab, the coequalizer of two group homomorphisms \(\phi, \psi: G \to H\) is the homomorphism

\[ \pi: H \to H/\im(\phi - \psi). \]

where \(g' \in H\) maps to the coset \(g' + \im(\phi - \psi)\). We show this as follows.

  • \(\bm{\pi \circ \phi = \pi \circ \psi}\). First let \(g \in G\), and consider the elements
\[\begin{align*} \pi\circ \phi(g) &= \phi(g) + \im(\phi - \psi)\\ \pi\circ \psi(g) &= \psi(g) + \im(\phi - \psi). \end{align*}\]

If we subtract these two quantities, we get that

\[\begin{align*} \pi \circ \phi(g) - \pi \circ \psi(g) &= \big[\phi(g) + \im(\phi- \psi)\big] - \big[\psi(g) + \im(\phi- \psi)\big]\\ &= (\phi(g) - \psi(g)) + \im(\phi- \psi)\\ &= 0 + \im(\phi - \psi). \end{align*}\]

Since their difference is zero, we see that they're equal. Hence \(\pi \circ \phi = \pi \circ \psi\). * Universality. Let \(f: H \to H'\) be another group homomorphism such that \(f \circ \phi = f \circ \psi\). Then construct the morphism \(f': H/\im(\phi - \psi) \to H'\) where

\[ h + \im(\phi - \psi) \longmapsto f(h). \]

Clearly this is well defined, since if \(h + \im(\phi - \psi) = h' + \im(\phi - \psi)\), then this means that \(h = h' + (\phi - \psi)(g)\), so that

\[\begin{align*} f'(h + \im(\phi- \psi)) &= f(h)\\ &= f(h' + \phi(g) - \psi(g))\\ &= f(h') + f\circ\phi(g) - f\circ\psi(g)\\ &= f(h') \end{align*}\]

where in the last step we used the fact that \(f \circ \phi = f \circ \psi\). Thus we see that \(f'\) is a well-defined group homomorphism. Furthermore, note that \(f = f' \circ \pi\). To finally show that \(f'\) is unique, we suppose there exists another group homomorphism \(k:H/\im(\phi-\psi) \to H'\) such that \(f = k\circ \pi\). Then we see that \(f' \circ \pi = k \circ \pi\), which implies that \(f' = k\).

What we've shown is that for any \(f: H \to H'\) such that \(f \circ \phi = f \circ \psi\), there exists a unique morphism \(f' : H/\im(\phi - \psi) \to H'\) such that \(f = f' \circ \pi\). Thus we see that \(\pi\) has the universal property of being a coequalizer.