5.2. Inverse and Direct Limits.

In the previous example, we calculated the limit of the diagram indexed by \(\omega\op\). It turns out that in general, we can construct a lot of mathematical ideas by first modeling them as the limit of a functor \(F: J \to \cc\), where \(J\) is a partially ordered set. Thus we give a special name to this concept.

Let \(\cc\) be a category, and suppose the \(F: J\op \to \cc\) has a limit object \(\Lim F\) in \(\cc\), where \(J\) is a partially ordered set (where, if \(i \le j\), then there exists \(f: i \to j\)). Then \(\Lim F\) is said to be a inverse limit or projective limit.

Dually, we define the colimit of a functor \(F: J \to F\) to be direct limit.

There are many famous examples of these limits, with the following example probably being the most familiar.

Consider the functor \(F: \omega\op \to **Rng**\) where we define \(F(n) = F_n = \zz/p^n\zz\) with \(p\) being a prime. Then we have a diagram

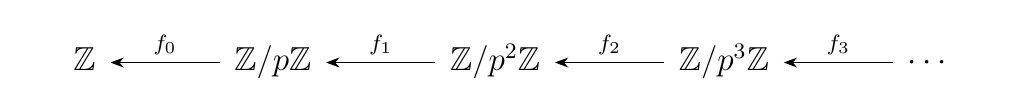where the maps \(f_n: \zz/p^{n+1}\zz \to \zz/p^n\zz\) are the projection maps. The limit of this diagram turns out to be the
**\(\bm{p**\)-adic integers} \(\zz_p\), and this is one way of defining them. The most popular way to define them it to work in ring theory, establish \(p\)-adic valuations, and realize that the valuations turn \(\zz\) into a metric space; one which can be completed with respect to the metric to give rise to \(\zz_p\).

First, observe that they form a cone. Define the map

\[ \pi_{n}: \zz_p \to \zz/p^{n}\zz \qquad \pi\left( \sum_{k = 0}^{\infty} a_kp^k \right) = \sum_{k =0}^{n-1}a_kp^k + p^{n}\zz. \]

Now observe that

\[\begin{align*} f_n \circ \pi_{n+1} \left( \sum_{k = 0}^{\infty}a_kp^k \right) = f_n\left( \sum_{k =0}^{n}a_kp^k + p^{n+1}\zz \right) &= \sum_{k =0}^{n-1}a_kp^k + p^{n}\zz\\ &= \pi_n\left( \sum_{k = 0}^{\infty}a_kp^k \right) \end{align*}\]

so we may conclude that \(f_n \circ \pi{n+1} = \pi_n\). Therefore, \(\zz_p\) does in fact form a cone with the morphisms \(\pi_n\), so the following diagram commutes.

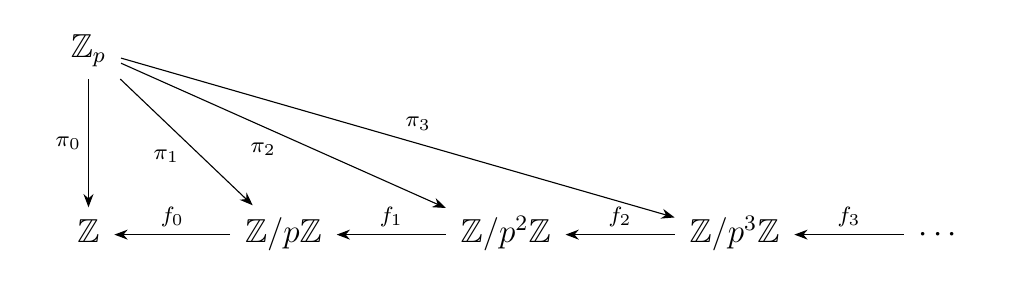Showing this is universal is simple once we realize that each element of \(\zz_p\) may be thought of as a cone, in the same fashion as we did with Set. That is, we can just apply the previous theorem to Rng. This then shows that it's the universal object which we desire.

What about direct limits? A less-talked about idea , although definitely not less interesting, is the dual of the above construction.

Consider the functor \(F: \omega \to **Grp**\) where we have \(F(n) = F_n = \zz/p^n\zz\), with \(p\) being a prime. This time however we have the diagram

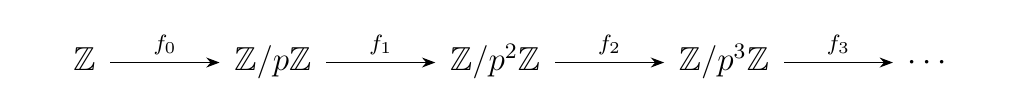where we define each \(f_n: \zz/p^n\zz \to \zz/p^{n+1}\zz\) as the homomorphism

\[ f_n\left( \sum_{k =0}^{n-1}a_kp^k + p^{n}\zz \right) = \sum_{k =0}^{n}a_kp^{k+1} + p^{n+1}\zz. \]

That is, we simply multiply the sum by a power of \(p\). It turn outs that the direct limit is the **Prüfer \(\bm{p**\)-Group} \(\zz(p^\infty)\). The Prüfer 2-Group is pictured below. \begin{center}

\end{center} The Prüfer \(p\)-group is the set of all \(p^n\) roots of unity, as \(n\) ranges over all positive integers. Hence the points lie on the complex unit circle. Specifically, it is the group

\[ \zz(p^{\infty}) = \left\{\text{exp}\left({\dfrac{2\pi i m}{p^n}}\right) \mid 0 \le m < p^n, n \in \mathbb{Z}^{+} \right\} \]

which forms a group under complex multiplication. How does this form a limit for our diagram?

Inverse limits are also used in Galois Theory. In Galois Theory, one can define a field extension \(L/F\) to be a finite, normal, separable extension. However, it turns out that one can remove the requirement for
the extension to be finite. We then obtain infinite Galois groups, which are constructed as follows.

Let \(F\) be a field, and suppose \(L/F\) is normal, separable extension (\textcolor{Red}{not necessarily finite!}). Then we can define \(L/F\) to be a Galois extension, and we may speak of a Galois group \(\gal(L/F)\), as follows.

Let \(\mathcal{F}(L/F)\) be the category of all finite, normal extensions \(K\) of \(F\) such that \(F \subset K \subset L\), and \(\mathcal{G}(L/F)\) is the category of all their Galois groups. Note that both \(\mathcal{F}(L/F)\) and \(\mathcal{G}(L/F)\) are partially ordered sets, ordered by subset inclusion. To be precise, if \(K_i \subset K_j\) are in \(\mathcal{F}(L/F)\), then

\[ \gal(K_j/F) \subset \gal(K_i/F) \]

and because \(\mathcal{G}(L/F)\) is a preorder on subset inclusion, this implies the existence of some arrow \(f: \gal(K_j/F) \to \gal(K_i/F)\). We can describe \(f = \proj_{K_j/K_i}\) where

\[ \proj_{K_j/K_i}: \gal(K_j/F) \to \gal(K_i/F) \qquad \proj_{K_j/K_i}(\sigma) = \sigma\big|_{K_i}. \]

That is, we take each permutation \(\sigma \in \gal(K_j/F)\) and restrict its action to \(K_i\), thereby making it a permutation of \(K_i\) which fixes \(F\), and therefore a member of \(\gal(K_i/F)\).

Now consider the product with the associated morphisms

\[ \prod_{K \in\mathcal{F}(L/F)}\gal(K/F) \qquad \pi_{K_i}: \prod_{K \in\mathcal{F}(L/F)}\gal(K/F) \to \gal(K_i/F) \]

Then we define

\[ \gal(L/F) = \left\{ x = (\cdots, \sigma_k, \cdots) \in \prod_{K \in \mathcal{F}(L/F)}\gal(K/F) \mid \proj_{K_i/K_j} \circ \pi_{K_i}(x) = \pi_{K_j}(x) \right\}. \]

So \(\gal(L/F)\) forms a cone with morphisms \(\pi_{K_i}\):

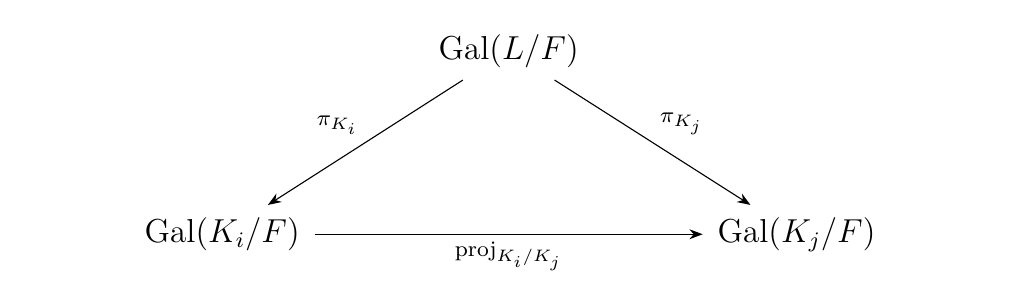We then have to work to show that this cone is universal. However, the faster route is to simply recognize that we can index \(\mathcal{G}(L/F)\) in a monotonic way, since it is a partially order set. Thus there exists a partially ordered set \(J\) such that if \(f: i \to j\) exists in \(J\), then

\[ F(i)= \gal(K_i/F) \quad F(j) = \gal(K_j/F) \implies F(f): \gal(K_i/F) \to \gal(K_j/F) \]

Thus we have a functor \(F: J \to \mathcal{G}(L/F)\) which hits every Galois group \(\gal(K/F)\) in such a way that it preserves the order in \(\mathcal{G}(L/F)\). Since the limit of every small diagram exists in Grp, we can define \(\gal(L/F)\) to be the inverse limit of this functor, and we already know that the limit will have the form

\[ \gal(L/F) = \left\{ (\cdots, \sigma_k, \cdots) \in \prod_{K \in \mathcal{F}(L/F)}\gal(K/F) \mid \proj_{K_i/K_j} \circ \pi_{K_i} = \pi_{K_j} \right\}. \]

and that it will be universal. So, this is how we extend the definition of Galois group from a finite, normal, separable extension to simple a normal, separable extension.

\noindent This construction can be done more generally on a partially ordered system of groups, to create these things called profinite groups.

Suppose we are given a partially ordered set of finite groups \(G_i\), indexed by some set \(I\), equipped with morphisms \(\{f^j_i: G_j \to G_i \mid i, j \in I \quad i \le j\}\) such that

• 1. \(f_i^i: G_i \to G_i\) is the identity \(\id_{G_i}\)
• 2. \(f_i^j \circ f_j^k = f_i^k\).

Then we define the profinite group \(G\) of this system to be the inverse limit:

\[ G = \left\{(g_i)_{i \in I} \in \prod_{i \in I} G_i \ \mid f_i^j(g_i) = g_j \right\}. \]

Note that requiring \(f_i^j(g_i) = g_j\) is the same as requiring \(f_i^j\circ \pi_i(x) = \pi_j(x)\), where \(x \in G\), which is how we defined \(\gal(L/F)\). \textcolor{MidnightBlue}{Thus in the previous example, we have that not only can we actually define \(\gal(L/F)\), but our construction leads to it to becoming a profinite group. Profinite groups are actually very special, in that they can be interpreted topologically.}