Des

I have been reading Applied Cryptography by Bruce Schneider, although not too seriously because it is very outdated. It is still useful because there really aren't many books on Cryptography or any books that actually explain implementations. While reading about block ciphers, I found it helpful to actually implement DES in order to understand what Schneider is saying when it comes to design, security, and attacks on encryption algorithms.

Background

The DES algorithm uses a symmetric-key and is a (64 bit)-block cipher that was once used very widely for encryption. By symmetric-key I mean there's one private key used to both encrypt and decrypt the data, and it does so by acting 64 bit blocks of the data. Exactly how that key is generated and how DES performs cumultaively on data longer than 64 bits are general separate problems for encryption algorithms and block ciphers.

DES Security

DES uses a 64-bit key, but that isn't actually the "true key" in the algorithm. The true key is a 56-bit key obtained from the 64-bit key by ignoring every 8th bit. This makes the algorithm weaker and, according to Schneider, was partly due to the NSA's involvement in the algorithm's development. Schneider speculates that the NSA wanted this to ensure they could utilize sophisticated and expensive hardware to brute force communications if they ever wanted to. As time went on this seemed plausible as researchers created proof of concept hardware specifically desgined for fast DES brute forcing that was within a country's intelligence budget.

However, Schneider also notes that for a period of time there were many attempts by researchers to come up with a better DES, but these replacements were usually pointed out to be weaker by other researchers, and most feasible attacks on DES were usually on a smaller numbers of rounds. So it seems the NSA did something right. Much later did more sophisticated attacks become possible and today the algorithm can be easily brute forced since the necessary hardware to do so has become cheaper over time.

How it works

DES performs 16 repetitions of a sequence of procedures, and these are called "rounds". The $i$-th round takes in two 32 bit blocks $L_i$, $R_i$, and a 48 bit key $K_i$. Each $K_i$ is generated from the secret key $K$ by a separate procedure. During a round we use a function $f$ to compute $f(R_i, K_{i+1})$. We then set \begin{align} L_{i+1} &= R_i\\ R_{i+1} &= L_i \oplus f(R_i, K_{i+1}) \end{align} (where $\oplus$ denotes XOR) and use these quantities for the next round. The last round is slightly different. Below is an overview of how the whole thing works.

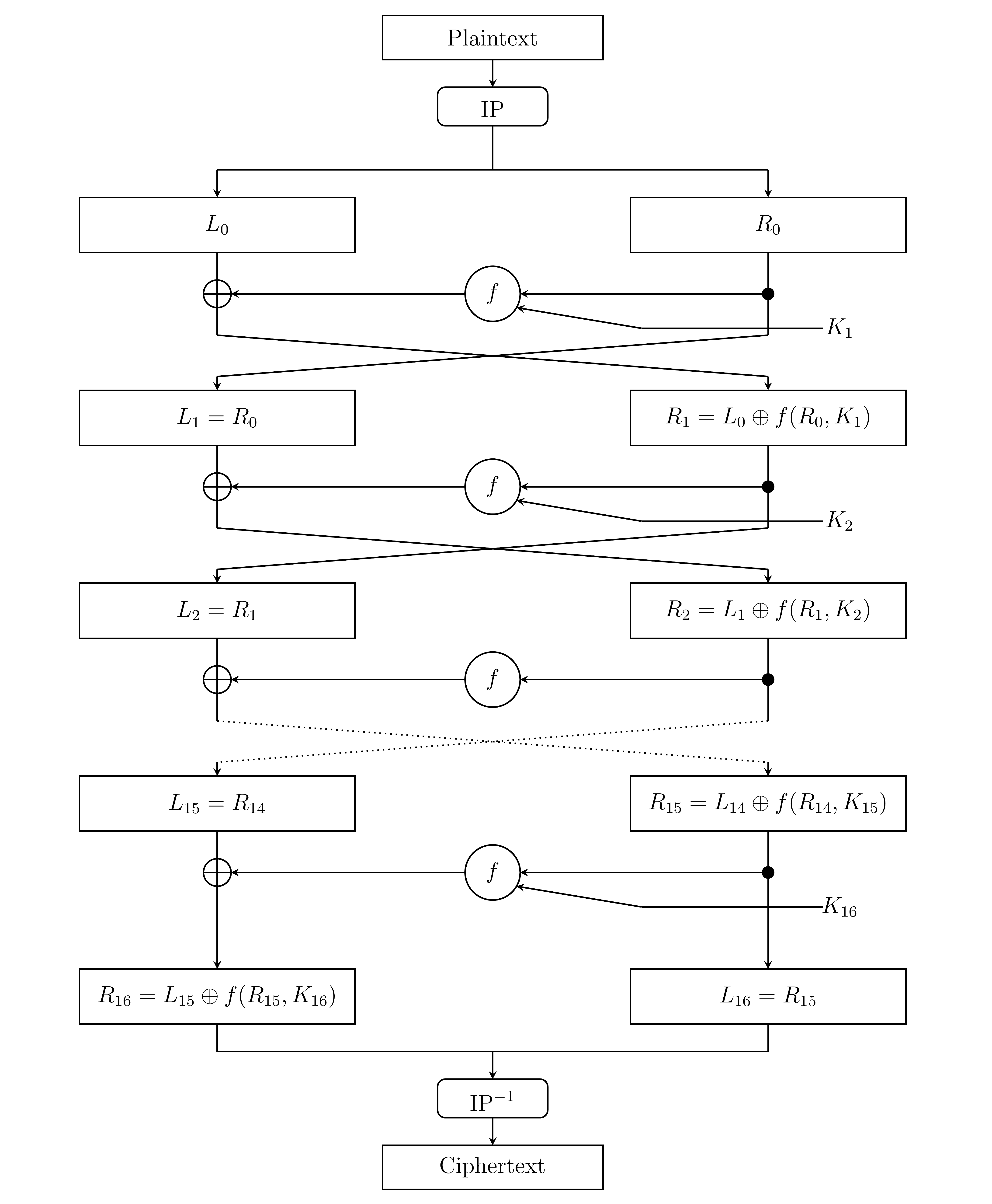
Generating L_0, R_0

To generate $L_0$ and $R_0$, we take the 64 bit input and apply an initial permutation (denoted by IP in the diagram above). The initial permutation is given below.

initial_perm = [
    58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4,
    62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8,
    57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3,
    61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7
]

So for example, the 58-th bit is reassigned to be the 1st bit, the 50-th bit is reassigned to be the second, and so on. Then, we let $L_0$ and $R_0$ be the left and right 32 bit halves of the permuted 64 bit block.

Generating the keys K_i

The $i$-th round takes in a 48 bit key $K_i$ which can be generated on the fly or once before the algorithm. It is calculated as follows.

First, we take the 64 bit key $K$ and apply a permutation that ignores every 8th bit to obtain a 56 bit key $K'$. That permutation is given below.

# The initial permutation reducing the 64 bit key to a 56-bit subkey
key_perm = [
    57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18,
    10, 2, 59, 51, 43, 35, 27, 19, 11, 3, 60, 52, 44, 36,
    63, 55, 47, 39, 31, 23, 15, 7, 62, 54, 46, 38, 30, 22,
    14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 28, 20, 12, 4
]

Then we split $K'$ into two halves and circularly shift the bits of these left and right halves to the left. The number of bits to shift depends on the round, and is given by the table below.

# The size of the circular shift to do in each round
num_key_shifts = [
    1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1
]

Call the circularly shifted halves $K_i^{(l)}$ and $K_i^{(r)}$. The next step is to take the concatenation of the two halves, $K_i^{(l)}K_i^{(r)}$, and apply a compression permutation which reduces the 56 bit concatenation to 48 bits. This becomes $K_i$, and we set $K' = K_i^{(l)}K_i^{(r)}$ for the next calcualtion of $K_{i+1}$. The compression permutation is given below.

# The compression permutation to apply to the 56 bit key after circular shift
compression_perm = [
    14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10,
    23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2,
    41, 52, 31, 37, 47, 55, 30, 40, 51, 45, 33, 48,
    44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32
]

The DES rounds

Now that we know how $L_0$, $R_0$, and $K_i$ are calculated, all we need to know is how the function $f$ works.

The value $f(R_i, K_{i+1})$ is computed as follows. The first thing we do is apply an expansion permutation to the right half $R_i$, which produces a 48 bit value from $R_i$'s 32 bits by permuting and duplicating its bits. The expansion permutation is below.

# Expansion permutation to apply to right half of input
expansion_perm = [
    32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9,
    8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17,
    16, 17, 18, 19, 20, 21, 20, 21, 22, 23, 24, 25,
    24, 25, 26, 27, 28, 29, 28, 29, 30, 31, 32, 1
]

Call the result $E_i$. We then compute the XOR value $E_i \oplus K_i$, which is a 48-bit value. This result is then subjected to S-Box substitutions. (According to Schneider, this is primarily where the strength of DES comes from, and everything else is fluff compared to this step)

The S-box substitutions takes the 48 bit value $E_i\oplus K_i$ and returns a 32 bit value $S(E_i \oplus K_i)$. It does this by using 8 different S-boxes, which are displayed below.

# S-Boxes
sbox_1 = [
    14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
    0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
    4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
    15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13,
]

sbox_2 = [
    15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
    3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
    0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
    13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9
]

sbox_3 = [
    10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
    13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
    13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
    1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12
]

sbox_4 = [
    7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
    13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
    10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
    3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14
]

sbox_5 = [
    2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
    14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
    4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
    11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3
]

sbox_6 = [
    12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
    10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
    9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
    4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13,
]

sbox_7 = [
    4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
    13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
    1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
    6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12,
]

sbox_8 = [
    13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
    1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
    7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
    2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
]

Each S-box is assigned to work on a separate 6 bit sub-block of $E_i \oplus K_i$. $S_1$ is assigned to bits 1 through 6, $S_2$ to the bits 7 through 13, and so on. Each S-box replaces its 6 bits with a 4 bit value. Specifically, it replaces the 6 bits with some value in its table. Notice that all of the S-boxes have values between 0 and 15, hence these can all can be expressed as 4 bit numbers in binary.

The way that an S-box chooses a value in its table to replace the 6 bit value works as follows. Denote the S-box as $S_i$, and our six bits as $b_1$, $b_2$, $b_3$, $b_4$, $b_5$, $b_6$. First we compute the 2 bit value $b_1b_6$, which is a number from 0 to 3. Then we compute the 4 bit value $b_2b_3b_4b_5$ which is a number from 0 to 15. We then replace these 6 bits with the 4 bit value represented in row $b_1b_6$, column $b_2b_3b_4b_5$ of S-box $S_i$.

Once we replace each 6 bit chunk with a 4 bit chunk, we get a 32 bit value, which we may denote as $S(E_i \oplus K_i)$. We then permute the 32 bit value $S(E_i \oplus K_i)$ by the permutation below.

# The permutation for the result of the sbox operation
sbox_perm = [
    16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10,
    2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4, 25
]

and the result obtained is defined to be $f(R_i, K_{i+1})$.

The final round

We perform 16 rounds, which are all the same except the last round. In the last step of the last round, we instead let $R_{16} = L_{15}\oplus f(R_{15}, K_{16})$ and $L_{16} = R_{15}$. We then reconcatenate these two, and apply the inverse of original permutation (denoted by $\text{IP}^{-1}$ in the diagram above), which is given by the table below.

# The final permutation after the 16 rounds
final_perm = [
    40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31,
    38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 6, 29,
    36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27,
    34, 2, 32, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25,
]

This result is the cipher text.

Decryption

What is nice about DES is that the same algorithm can be used for decryption, except you use the keys $K_i$ in reverse order. This means that decryption is dead simple only if you have the private key, which is a good feature of a block cipher.

Python Code

Now that the algorithm details are explained, here comes the Python code. In this implementation we treat the binary values as a list of ones and zeros. The overall DES function can be described by this simple function.

Note the main function below is for both encryption and decryption. It accepts input and the fake key (i.e. the 64 bit secret key, which I called fake since some of its digits get ignored), and encrypts by default.

The first function we need for the above to work is a function to generate the keys $K_i$

The next function we need is DES_round, which computes a single round of DES.

The above function uses several helper functions: a function to do the S-box substitutions, a function

And that is it! name="__codelineno-8-1" href="#__codelineno-8-1">def DES(input: list[int], fake_key: list[int], decrypt: bool=False) -> list[int]: """The DES encryption algorithm.""" # Apply the initial permutation to the 64-bit input input = [input[new_pos - 1] for new_pos in initial_perm] # -1 since they count from 1, not 0. left = input[:32] right = input[32:] # Reduce the 64-bit key to a 56-bit subkey, then generate the 16 48 bit subkeys key = [fake_key[new_pos - 1] for new_pos in key_perm] sub_keys = generate_subkeys(key, decrypt) # Perform the 16 rounds of DES for round in range(0, 16): left, right = DES_round(left, right, sub_keys[round]) # For the last round, undo the swapping of the left and right blocks last_block = right + left last_block = [last_block[new_pos - 1] for new_pos in final_perm] return last_block used in the algorithm. name="__codelineno-9-1" href="#__codelineno-9-1">def generate_subkeys(key: list[int], decrypt: bool=False) -> list[list[int]]: """Generate the 16 keys used in the DES algorithm.""" sub_keys = [] for round in range(16): # Split the 56-bit key into two halves left_key_half = key[:28] right_key_half = key[28:] # Circularly shift the bits left, depending on the round shift = num_key_shifts[round] left_key_half = [left_key_half[ind % 28] for ind in range(shift, shift + 28)] right_key_half = [right_key_half[ind % 28] for ind in range(shift, shift + 28)] # Pick 48 out of the 56 circularly shift bits to form the compressed key compressed_key = [(left_key_half + right_key_half)[new_pos - 1] for new_pos in compression_perm] sub_keys.append(compressed_key) # Preserve the shift, repeat key = left_key_half + right_key_half return sub_keys name="__codelineno-10-1" href="#__codelineno-10-1">def DES_round(left_half: list[int], right_half: list[int], sub_key: list[int]) -> tuple: class="w"> """Performs a single round of DES.""" # Apply the expansion permutation to the right half, growing from 32 to 48 bits expanded_right = [right_half[ind - 1] for ind in expansion_perm] # XOR the compressed key and expanded right key_input_xor = XOR(sub_key, expanded_right) # Now we perform the sbox substitutions to obtain a 32 bit number sbox_res = [] sbox_res += sbox_subsitute(key_input_xor[: 6], sbox_1) sbox_res += sbox_subsitute(key_input_xor[6:12], sbox_2) sbox_res += sbox_subsitute(key_input_xor[12:18], sbox_3) sbox_res += sbox_subsitute(key_input_xor[18:24], sbox_4) sbox_res += sbox_subsitute(key_input_xor[24:30], sbox_5) sbox_res += sbox_subsitute(key_input_xor[30:36], sbox_6) sbox_res += sbox_subsitute(key_input_xor[36:42], sbox_7) sbox_res += sbox_subsitute(key_input_xor[42:48], sbox_8) # Permute the result from the sbox operation sbox_res_permute = [sbox_res[new_pos - 1] for new_pos in sbox_perm] # Finally we XOR this permutation with the left half of the input to obtain the right half for the next round next_round_right_half = XOR(left_half, sbox_res_permute) return right_half, next_round_right_half to convert a integer to a 4 bit binary number, and a function to compute XOR. name="__codelineno-11-1" href="#__codelineno-11-1">def sbox_subsitute(input: list[int], sbox: list[int]) -> list[int]: class="w"> """Return the 4 bit value in sbox to replace the 6 bit input value.""" row = 2*input[0] + input[5] column = 8 * input[1] + 4 * input[2] + 2 * input[3] + input[4] return four_bit_binary(sbox[row * 16 + column]) class="k">def four_bit_binary(integer: int) -> list[int]: class="w"> """Convert an integer from 0 to 15 to a list of 4 bits.""" return [int(bit) for bit in format(integer, '04b')] class="k">def XOR(A: list[int], B: list[int]) -> list[int]: class="w"> """Simple XOR function.""" assert len(A) == len(B) xor_val = [] for i in range(len(A)): a = A[i] b = B[i] xor_val.append(int((a or b) and not (a and b))) return xor_val

An Example

Testing that this works is actually tricky, since most "online DES encoder/decoders" are simply incorrect garbage. Fortunately, I found an example of a DES computation on this website. In the example provided, the message to decode is $M = 0123456789\text{ABCDEF}$, or $$ M = 00000001 \ 00100011 \ 01000101 \ 01100111 \ 10001001 \ 10101011 \ 11001101 \ 11101111 $$ in binary. They then used the hexidecimal key $133457799\text{BBCDFF}1$, which in binary is $$ K = 00010011 \ 00110100 \ 01010111 \ 01111001 \ 10011011 \ 10111100 \ 11011111 \ 11110001 $$ The encrypted message becomes $$ C = 10000101 \ 11101000 \ 00010011 \ 01010100 \ 00001111 \ 00001010 \ 10110100 \ 00000101 $$ We can put the message, key in a list of integers

input = [0, 0, 0, 0, 0, 0, 0, 1, 
         0, 0, 1, 0, 0, 0, 1, 1, 
         0, 1, 0, 0, 0, 1, 0, 1, 
         0, 1, 1, 0, 0, 1, 1, 1, 
         1, 0, 0, 0, 1, 0, 0, 1,
         1, 0, 1, 0, 1, 0, 1, 1, 
         1, 1, 0, 0, 1, 1, 0, 1,
         1, 1, 1, 0, 1, 1, 1, 1]

key   = [0, 0, 0, 1, 0, 0, 1, 1, 
         0, 0, 1, 1, 0, 1, 0, 0, 
         0, 1, 0, 1, 0, 1, 1, 1,
         0, 1, 1, 1, 1, 0, 0, 1, 
         1, 0, 0, 1, 1, 0, 1, 1,
         1, 0, 1, 1, 1, 1, 0, 0, 
         1, 1, 0, 1, 1, 1, 1, 1,
         1, 1, 1, 1, 0, 0, 0, 1]

and running DES(input, key) returns the value

[1, 0, 0, 0, 0, 1, 0, 1,
 1, 1, 1, 0, 1, 0, 0, 0,
 0, 0, 0, 1, 0, 0, 1, 1,
 0, 1, 0, 1, 0, 1, 0, 0,
 0, 0, 0, 0, 1, 1, 1, 1, 
 0, 0, 0, 0, 1, 0, 1, 0, 
 1, 0, 1, 1, 0, 1, 0, 0, 
 0, 0, 0, 0, 0, 1, 0, 1]

which matches the message. Decrypting this produces our original cipher text:

DES()

The author also points out that the message hexidecimal message M = 8787878787878787" encrypted with the DES key "0E329232EA6D0D73" produces the cipher text "0000000000000000", which also checks out with our function.