3.6. Free $R$-modules.

Free modules are the type of modules that you are probably already familiar with. Basically, they're modules who have some kind of generating set, which can create all other elements. As we can think of modules as vector spaces, we know that vectors spaces always have some kind of basis set, at least when they can be thought of as existing in $\RR^n$. It turns out that having a basis leads to many desirable properties.

First, we make a definition on linear independence, a concept required for discussing bases, and then formally define a free module.

Let $R$ be a ring and $M$ an $R$-module. Then the set $S = \{x_1, x_2, \dots, x_n\}$ with $S \subset M$ is said to be linearly independent if and only if the only solution to the equation

\[ a_1x_1 + a_2x_2 + \cdots + a_nx_n = 0 \]

is $a_1 = a_2 = \cdots = a_n = 0$ (where $a_1, a_2, \dots, a_n \in R$).

If $S$ is the smallest linear independent subset of $M$, then we say that $S$ is a basis for $M$, in which case $M$ is said to be a free $R$-module. Hence, an $R$-module is a module with a basis.

This is the exact same definition of linear independence we've seen in linear algebra. Nothing is new here. It is a classic exercise in linear algebra to check the following statement, which we offer here.

$S$ is a basis for some $R$-module $M$ if and only if every $x \in M$ can be written uniquely as

\[ x = a_1x_1 + a_2x_2 + \dots a_nx_n \]

where $a_i \in R$ and $x_i \in S$ for $i = 1,2, \dots, n$.

Examples

1. Consider the $R$-module $M_{m,n}(R).$ Observe that a basis for this module consists of

$$ {E_{ij} \mid 1 \le i \le m, 1 \le j \le n}. $$ * 2. Consider an abelian group $G$. Then as we showed before, $G$ is technically a $\mathbb{Z}$-module. However, if $G$ is finite, then it is not a free $\ZZ$-module.

Suppose to the contrary that it is, and that $S = \{x_1, x_2, \dots, x_n\}$ is a linearly independent set which forms a basis of $G$. Then if $\{o_1, o_2, \dots, o_n\}$ is a set such that $o_i = \text{order}(x_1)$ (which exists, by finiteness of $G$) then

\[ o_1x_1 + o_2x_2 + \cdots + o_nx_n = 0. \]

Hence, the set $\{x_1, x_2, \dots, x_n\}$ is not linearly independent, so $G$ is not a free $\ZZ$-module. * 3. Consider the set $R[X]$. Observe that a suitable generating basis is

\[ \{x^n \mid n \in \mathbb{N}\} \]

which is probably something you already knew. * 4. Suppose $M_1$ and $M_2$ are free modules with bases $S_1, S_2$. Then the set $M_1 \oplus M_2$ is a free module, since it has a basis

\[ \{(x, 0) \mid x \in S_1\} \cup \{(0, y) \mid y \in S_2\}. \]

More generally, if $\{M_\alpha\}_{\alpha \in \lambda}$ is a of free modules where $S_\alpha$ is the basis of $M_\alpha$, then we see that

\[ \oplus_{\alpha \in \lambda}M_\alpha \]

is also a free module with basis

\[ \bigcup_{\alpha \in \lambda}\{(\delta_{jk}s_{j\alpha}) \mid s_{j\alpha} \in S_j\}. \]

where $\delta_{jk}$ is the Kronecker delta function.

Let $M$ be a free $R$-module. Suppose the basis of the set is $S$. Let $N$ be an $R$-module and $h: S \to N$ a function. Then there exists a function $f \in \hom_R(M, N)$ such that $f\mid_S = h$.

Let $R$ be commmutative and $M$ and $N$ free modules with bases. Then $\hom_R(M, N)$ is a finitely generated free module.

Suppose the basis for $M$ is $S = \{x_1, x_2, \dots, x_n\}$, and the basis for $N$ is $T = \{y_1, y_2, \dots, y_m\}$. Define a set of functions for $1 \le i \le m$ and $1 \le j \le n$ such that

\[ f_{ij}(x_k) = \begin{cases} y_j & \text{ if } k = i\\ 0 & \text{ if } k \ne j \end{cases}. \]

By the previous proposition, we know that each $f_{ij}$ is a element in $\hom_R(M, N)$. Now let $f \in \hom_R(M,N)$ be arbitrary. Since $T$ is a basis for $N$, we know that for each $v_k \in S$ there exists coefficients $a_{k1}, a_{k2}, \dots, a_{kn}$ such that

\[ f(v_k) = a_{k1}y_1 + \cdots + a_{kn}y_n. \]

However, observe that

\[\begin{align*} f(v_k) &= a_{i1}y_1 + \cdots + a_{in}y_n\\ &= a_{k1}f_{k1}(x_k) + a_{k2}f_{k2}(x_k) + \cdots + a_{kn}f_{kn}(x_k). \end{align*}\]

Therefore, we see that for any $b \in M$,

\[\begin{align*} f(b) &= f(a_{b1}x_1 + \cdots + a_{bm}x_m)\\ &= a_{b1}f(x_1) + \cdots + a_{bm}f(x_m)\\ &= a_{b1}[a_{11}f_{11}(x_1) + a_{12}f_{12}(x_1) + \cdots + a_{1n}f_{1n}(x_1)]\\ &\hspace{.6cm} + a_{b2}[a_{21}f_{21}(x_2) + a_{22}f_{22}(x_2) + \cdots + a_{2n}f_{2n}(x_2)]\\ &\hspace{.6cm} + \cdots\\ &\hspace{.6cm} + a_{bm}[a_{m1}f_{m1}(x_m) + a_{m2}f_{m2}(x_2) + \cdots + a_{mn}f_{mn}(x_m)]. \end{align*}\]

Therefore we see that $\{f_{ij}\}$ generates $\hom_R(M, N)$, so that $\hom_R(M, N)$ is finitely generated. The previous theorem doesn't hold if $M$ and $N$ are not finitely generated, since there are many counter examples to such a claim. \textcolor{purple}{ Let $R = \mathbb{Z}$ and $M = \oplus_{i = 1}^{\infty}\mathbb{Z}$. Then observe that

\[ \hom_R(M, \ZZ) \cong \prod_{i = 1}^{\infty}\ZZ. \]

by Theorem 1.13. However, we see that while $\ZZ$ is finitely generated and $M$ is finitely generated, but $\displaystyle \prod_{i = 1}^{\infty}\ZZ$ is not. (The proof is nontrivial.)}

Let $M$ be a free $R$-module with basis $S = \{x_j\}_{j \in J}$ and suppose $I$ is an ideal of $R$. Let $\pi: M \to M/I$. Then $M/IM$ is a $R/I$-module and is free with basis $\pi(S) = \{ \pi(x_j)\}_{j \in J}$.

$\bm{M/IM}$ is an $\bm{R/I}$-module. First recall that $IM$ is a submodule of $M$. Therefore it makes sense to consider the quotient $M/IM$. Then we can define a mapping $\cdot: R/I \times M/IM \to M/IM$ as follows. Let $r
I \in R/I$ and $m + IM \in M/IM$. Then define the mapping as

\[\begin{align*} (r + I)\cdot(m + IM) &= r(m + IM)\\ &= rm + rIM\\ &= rm + IM. \end{align*}\]

Since $M$ is an $R$-module, $rm \in M$ so that $rm + IM$ is in fact in $M/IM$. The other module properties may be easily verified without difficulty by using this mapping. * $\bm{M/IM}$ is free. Suppose $m+ IM$ is an element of $M/IM$. Since $\pi: M \to M/I$ is a surjective mapping, we see that there exists at least one $m \in M$ such that $\pi(m) = m + IM$. Now since $m$ is free, there exists a unique representation of $m$ of its basis elements, i.e., there exists $\{a_j\}_{j \in J}$, a subset of $R$, such that

\[ m = \sum_{j \in J} a_jx_j \implies \pi(m) = \pi\left(\sum_{j \in J} a_jx_j \right) = \sum_{j \in J} a_j\pi(x_j) + IM \]

Hence $m + IM = \sum_{j \in J} a_j\pi(x_j) + IM.$ To finish showing that $\{\pi(x_j)\}_{j \in J}$ is a basis for $M/IM$, we only have to show that it is a linearly independent set. So consider the equation

\[ \sum_{j \in J}a_j\pi(x_j) = 0 + IM \]

for some constants $\{a_j\}_{j \in J}$ in $\mathbb{R}$. Suppose additionally for contradiction that not all of the constants are nonzero. Then we that $\sum_{j \in J}a_j\pi(x_j)$ is an element of $IM$. However, this is a contradiction since none of the elements of $\{\pi(x_j)\}_{j \in J}$ is allowed to be in $IM$. Hence this set generates $M/IM$ and is linearly independent, so it is a basis.

We can introduce an even more useful proposition regarding free modules, and more generally all modules.

Let $M$ be an $R$-module. Then

\[ M \cong F/K \]

for a free module $F$ and some submodule $K$ of $F$. That is, $M$ is the quotient of some free module $F$. Furthermore, if $M$ is finitely generated, then such an $F$ is finitely generated and $\mu(F) = \mu(M)$.

Suppose $S = \{x_j\}_{j \in J}$ is a set of elements which generate $M$. Note that, even in the worst case scenario, such an $S$ exists since we can at most take $S = M$. Now suppose $F = \oplus{j \in J}R$, which is a free module. Construct the module homomorphism $\psi: F \to M$ as

\[ \psi((a_j)_{j \in J}) = \sum_{j \in J} a_jx_j. \]

Observe that since $S$ generates $M$, such a homomorphism is surjective onto $M$. Hence, we see that $M$ is the quotient of some free module $F$.

Now suppose that $F$ is finitely generated. Then $S$ is a finite set, so that $F$ is also finitely generated (since in this case it is the direct sum of at most a finite number of copies of $R$).

Now if $M$ is finitely generated, and is a quotient of $F$, then clearly $\mu(M) \le \mu(F)$. However, we also know that $\mu(F) \le |J| \le \mu(M)$. Therefore, we see that $\mu(M) = \mu(F)$.

Let $M$ be an $R$-module and $F$ a free $R$-module. Then the short exact sequence

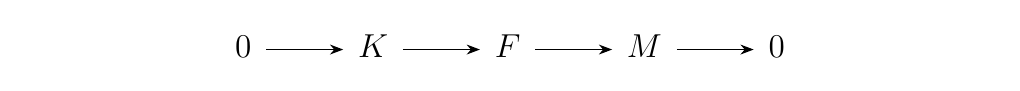is called a free presentation of $M$. Note by the previous proposition that every $R$-module has a free presentation.

Presentations are particularly useful since they make free modules convenient to work with.

Suppose $F$ is a free $R$-module. Then every short exact sequence

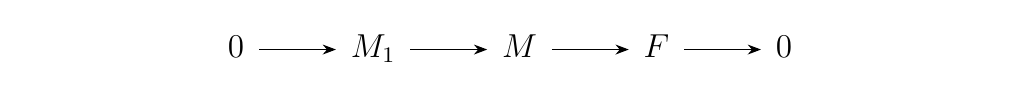is a split exact sequence.

Let $S = \{x_j\}_{j \in J}$ be a basis for $F$. Now suppose $f: M \to F$ is the surjective function in the above exact sequence. Now construct a function $\psi: F \to M$ as follows: $\psi(x_j) = m_j$ if and only if $f(m_j) = x_j$. Since $f$ is surjective, note that this will always be possible. Such a function may not be unique, but we don't care; we just want to know it exists.

By proposition \ref{prop: unique homomorphism}, we know that there exists a unique function $h: F \to M$ such that $h|_S = \psi$. Therefore we see that $f \circ h = 1_F$, so that by theorem \ref{split_exact_lemma}, we see that the sequence is in fact split exact.

3.6. Free \(R\)-modules.