3.4. Finite Coproducts

We now move onto the concept of coproducts in categories. We will see that this concept is an instance of a colimit, which is yet to be defined. We build intuition on the concept with the special concept of coproducts by introducing examples.

Let \((G, \textcolor{NavyBlue}{\bigcdot})\) and \((H, \textcolor{Orange}{\bigcdot})\) be two groups with group operations $\textcolor{NavyBlue}{\bigcdot}: G \times G \to G $ and \(\textcolor{Orange}{\bigcdot}: H \times H \to H\). The free product of \(G\) and \(H\) is the group

\[ (G \* H, \bigcdot) = \bigg\{ g_1h_1g_2h_2\cdots g_kh_k \;\bigg|\; g_i \in G, h_i \in H \bigg\} \]

with the following operation. If \(g_1h_1\cdots g_kh_k\) and \(g'_1h'_1\cdots g'_{\ell}h'_{\ell}\) are two elements of \(G \* H\), then

\[ (g_1h_1\cdots g_kh_k) \mathbin{\bigcdot} (g'_1h'_1\cdots g'_{\ell } h'_{\ell } ) = g_1h_1\cdots g_kh_k g'_1h'_1 \cdots g'_{\ell}h'_{\ell}. \]

We require the group operation to obey the following two rules. Let \(g_1h_1\cdots g_kh_k \in G \* H\).

• If \(g \in G\), then

$$ g \mathbin{\bigcdot} (g_1h_1\cdots g_kh_k) = (g \mathbin{\textcolor{NavyBlue}{\bigcdot}} g_1)h_1\cdots g_kh_k. $$ * If \(h \in H\), then

\[ (g_1h_1\cdots g_kh_k)\mathbin{\bigcdot} h = g_1h_1\cdots g_k(h_k \mathbin{\textcolor{Orange}{\bigcdot}} h). \]

The free product of two groups arise frequently in algebraic topology. Despite that its definition is somewhat complicated, we will see later that free products are in some sense dual to the concept of the product of groups. The reader will also soon see that the naming "free product" is an unfortunate one as it is somewhat misleading.

Free products appear prominently in various statements of Van Kampen's theorem in topology; what follows is a simplified version. If \(X = U \cup V\) is a topological space with \(U, V\) open sets, and if \(U \cap V \ne \varnothing\) is path connected and simply connected, then

\[ \pi_1(X) \cong \pi_1(U)\* \pi_1(V) \]

where \(\pi_1(X)\) is the fundamental group of \(X\). (Note that since \(X\) is path connected, it doesn't matter what basepoint for the fundamental group we select).

We will soon see that the free product is the coproduct in the category of Grp, although such a statement should not make any sense the reader until we define what a coproduct is.

In Set, we can combine two different sets \(X\) and \(Y\) to create the disjoint union \(X \amalg Y\), which is defined to be the set

\[ X \amalg Y = \bigg\{ (x, 0), (y, 1) \;\bigg|\; x \in X, y \in Y \bigg\}. \]

In the above set, elements are tuples whos first coordinate is either in \(X\) or \(Y\), and the second is some value which depends on whether or not the first coordinate is in \(X\) or \(Y\). I decided to make these values 0 and 1, but it is ultimately arbitrary. We just need to make sure that these values are distinct so that we can determine if a tuple has an element from \(X\) or \(Y\) based on the value in the second slot. For example, for a tuple \((z, 0)\), we know that \(z \in X\). If the tuple is of the form \((z, 1)\), we know that \(z \in Y\).

We perform a similar analysis as before with products, and we consider the following question. \begin{center} \begin{minipage}{0.8\textwidth} Q: What is the bare minimum amount of logical data that perfectly characterizes the above disjoint union \(X \amalg Y\)?
\end{minipage} \end{center} Observe that we have the two inclusion functions

\[\begin{align*} &i_1: X \to X \amalg Y \qquad i_1(x) = (x, 0)\\ &i_2: Y \to X \amalg Y \qquad i_2(y) = (y, 1). \end{align*}\]

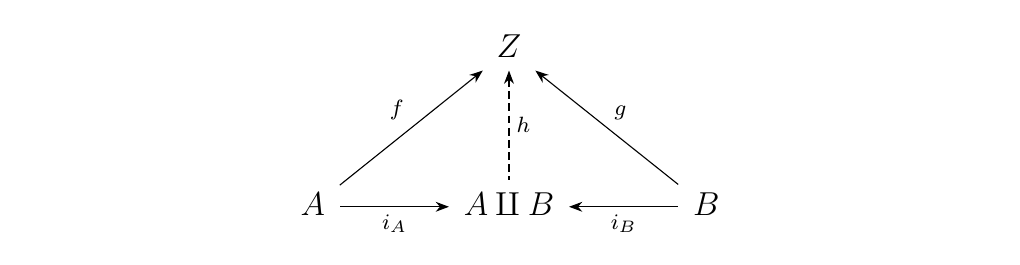
These two functions are equipped with the following remarkable property. Let \(Z\) be some set, and suppose I have two functions

\[\begin{align*} &f: X \to X \amalg Y \\ &g: Y \to X \amalg Y. \end{align*}\]

Then there exists a unique function \(h: X \amalg Y \to Z\) such that the diagram below commutes.

\begin{align}

\qquad h(z, i) = \begin{cases} f(z) & \text{if } i = 0\ g(z) & \text{if } i = 1 \end{cases} \end{align}

This definition of this unique \(h: X \amalg Y \to Z\) is described above on the right. With the above definition, one can easily see that the above diagram does in fact commute. We now have an answer to our question. \begin{center} \begin{minipage}{0.8\textwidth} A: The disjoint union \(X \amalg Y\) is characterized by two inclusion functions \(i_1: X \to X \amalg Y\), \(i_2: Y \to X \amalg Y\), such that, for any \(f: X \to Z\), \(g: Y \to Z\), there exists a unique \(h: X \amalg Y \to Z\) such that diagram \ref{diagram:disjoint_union_diagram} commutes. \end{minipage} \end{center}

This now motivates the following definition of a coproduct.

[Nice Coproduct Definition.] Let \(\cc\) be a category with objects \(A\) and \(B\). The coproduct of \(A\) and \(B\) is an object \(A \amalg B\) of \(\cc\) which is equipped with morphisms

\[ i_A: A \to A \amalg B \qquad i_B: B \to A \amalg B \]

with the following universal property: For any object \(Z\) of \(\cc\) with a pair of morphisms \(f: A \to Z\) and \(g: B \to Z\), then there exists a unique morphism \(h: A \amalg B \to Z\) such that the diagram below commutes.

It is now clear that, coproducts in Set exist; it is the disjoint union.

Note that to utilize the above universal property, one requires a pair of morphisms \(f: A \to Z\) and \(g: B \to Z\). That is, it is not true that, if I have a single morphism \(k: A \to Z\), then there exists a unique \(h: A \amalg B \to Z\) such that \(h \circ i_X = k\). That would be false in many cases.

Suppose \(\cc\) is a category with an initial object \(I\) and a coproduct object \(A \amalg B\) for every pair of objects \(A\) and \(B\). Then

• \(\bm{(i)}\) \(\cc\) has finite coproducts.
• \(\bm{(ii)}\) There exists a bifunctor \(\amalg: \cc \times \cc \to \cc\) where \((A, B) \mapsto A \amalg B\).
• \(\bm{(iii)}\) For any three objects, we have an isomorphism

\[ (A \amalg B) \amalg C \cong A \amalg (B \amalg C) \cong A \amalg B \amalg C \]

which is natural in \(A, B\) and \(C\) . * \(\bm{iv}\) For any object \(A\), we have the isomorphism

\[ I \amalg A \cong A \cong I \amalg A \]

natural in \(A\), where \(T\) is the initial object of the category.

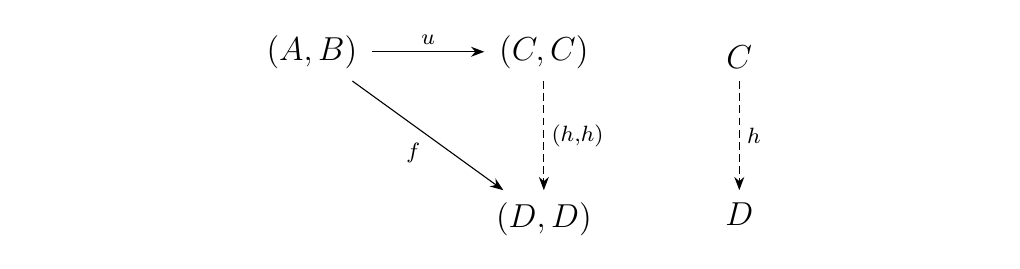
[Rigorous Coproduct Definition] Let \(\cc\) be a category with objects \(A, B\). The coproduct \(A \amalg B\) of \(A\) and \(B\) is a universal morphism

\[ (A \amalg B, i: (A,B) \to \Delta(A \amalg B)) \]

from \hyperref[definition:universal_morphism_from_F_to_D]{\textcolor{blue}{\((A,B)\) to \(\Delta\)}}. This means that, for any other pair \((C, j: (A, B) \to \Delta(C))\), there exists a unique \(h: A \amalg B \to C\) such that the diagram below commutes.

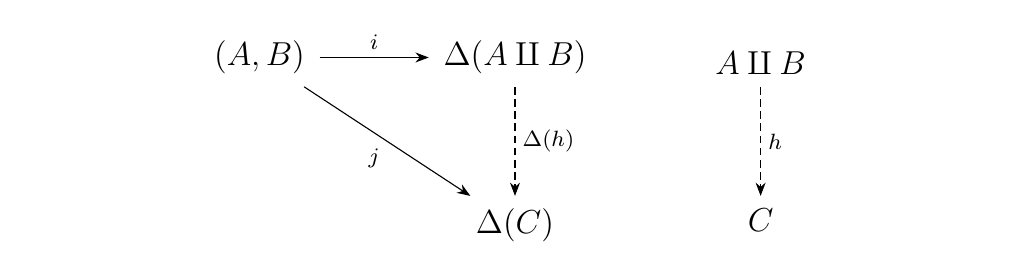
Visually, we have that