10.3. Stalks and Germs
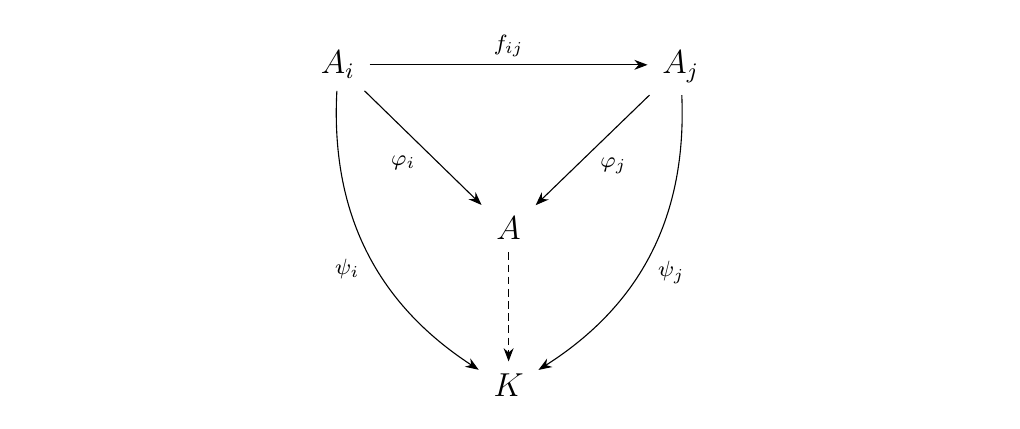
Let \((I, \le)\) be a partially ordered set, and suppose we have a functor \(F: I \to **Set**\). With this functor, denote \(F(i) = A_i\) and when \(i \le j\), \(F(i \le j) = f_{ij}: A_i\to A_j\). The limit of this functor \(\displaystyle \Limto_{i \in I} F\) will be a set \(A\) equipped with functions \(\phi_i: A_i \to A\) with the universal property displayed below.
 We may naively suppose that \(\displaystyle A = \coprod_{i \in I}A_i = \{(a, i) \mid a \in A_i, i \in I \}\), since such a set
admits a family of functions \(\displaystyle \text{inc}_i: A_i \to \coprod_{i \in I}A_i\).
However, we cannot guarantee that this the triangle
We may naively suppose that \(\displaystyle A = \coprod_{i \in I}A_i = \{(a, i) \mid a \in A_i, i \in I \}\), since such a set
admits a family of functions \(\displaystyle \text{inc}_i: A_i \to \coprod_{i \in I}A_i\).
However, we cannot guarantee that this the triangle
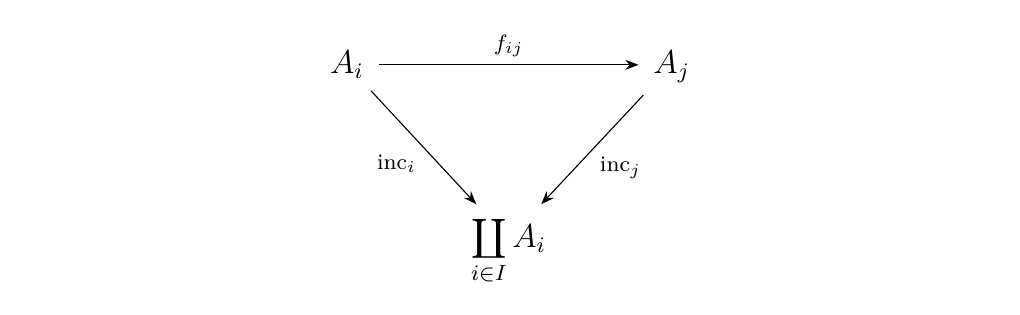 will commute. In fact, it will never commute, since it would imply that
for each \(a \in A_i\), \((a, i) = (f_{ij}(a), j)\), which cannot happen as the
tuples are mismatched. Since it is too strong to demand equality, we can define
an equivalence relation \(\sim\) on \(\displaystyle \coprod_{i \in I}A_i\)
as follows: For \(i \le j\), we say \((a, i) \sim (b, j)\) if
\(b = f_{ij}(a)\). We can then set
will commute. In fact, it will never commute, since it would imply that
for each \(a \in A_i\), \((a, i) = (f_{ij}(a), j)\), which cannot happen as the
tuples are mismatched. Since it is too strong to demand equality, we can define
an equivalence relation \(\sim\) on \(\displaystyle \coprod_{i \in I}A_i\)
as follows: For \(i \le j\), we say \((a, i) \sim (b, j)\) if
\(b = f_{ij}(a)\). We can then set
and define a family of maps \(\phi_i: A_i \to A\) which maps each \(a \in A_i\) to its equivalence class under this relation. This then allows the desired triangle to commute and satisfies the universal property necessary for it to be the limit.
We now apply this construction to our story with sheaves.
Let \(X\) be a topological space and \(F: \mathcal{O}(X) \to **Set**\) a sheaf. For any point \(x \in X\), we define the stalk of \(F\) in \(x\), denoted \(F_x\), as the colimit
The above notation is a bit informal, but many people use it, so we will stick with it and explicitly describe this limit as follows. Each point \(x \in X\) induces a functor \(F^{(x)}: \mathcal{O}(X)_x \to **Set**\) where \(\mathcal{O}_x\) is the category of open sets of \(X\) containing \(x\), and \(F^{(x)}(U) = F(U)\). We can then more formally say
Therefore, we can say that
where \(\sim\) is the equivalence relation described previously. In this instance, the equivalence relation translates as follows. Let \(U_1 \subset U_2\) be two open sets. Then we say \((f, U_1) \sim (g, U_2)\) if \(g\Big|_{U_1} = f\).
We can make this more refined as follows. Let \(U_1, U_2\) be more generally any two open sets such that \(V = U_1 \cap U_2 \ne \varnothing\). Then clearly \(V \subset U_1\) and \(V \subset U_2\). Now suppose, \((f, V) \sim (g_1, U_1)\) for some \(f, g_1\), and \((f, V) \sim (g_2, U_2)\). Then we now have that
Thus we have translated our original equivalence relation into a more useful one. To summarize, we have that our stalk is the set
where \((f, U)\) is a representative of its equivalence class \([(f, U)]\), described explicitly as
The above line leads to our next definition.
Let \(U\) be an open set containing \(x\). There naturally exists projection map
Therefore, for each \(f \in F(U)\), we define
the germ of \(f\) in \(x\) to be the equivalence class
\([(f, U)]\) in the stalk \(F_x\).