7.7. Monoids, Groups, in Symmetric Monoidal Categories

Recall from section ? that we were able to construct monoid and groups which were internal to some category \(\cc\). The philosophy behind the construction is one we've seen before: we of course think of monoids and groups by their elements, but we resist the temptation and instead present an object-free, diagrammatic set of axioms for monoids and rings. We utilized the cartesian product in the category \(\cc\) to demonstrate this. However, we now know that the cartesian product in any category is a small example of a category with a symmetric monoidal structure. Hence we revisit the concepts of a monoid and group, and expand their generality by demonstrating that they can be defined in a symmetric monoidal category.

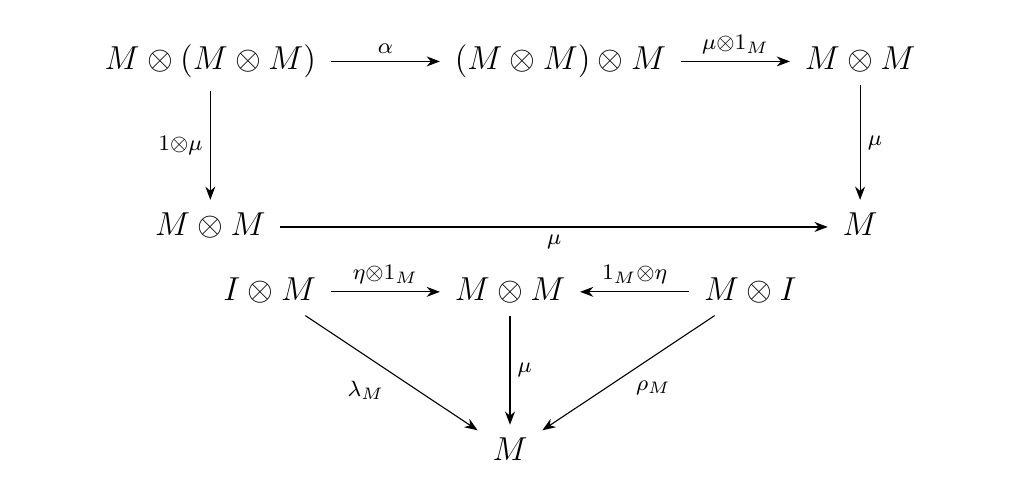
Let \((\mathcal{M}, \otimes, I, \alpha, \rho, \lambda)\) be a monoidal category and let \(M\) be an object of \(\mathcal{M}\). We say \(M\) is if there exist maps

\[\begin{align*} \mu&: M\otimes M \to M \\ \eta&: I \to M \end{align*}\]

referred to as the multiplication and identity maps, such that the diagrams below commute.

One of the most useful examples of this concept arises from the notion of an algebra \(A\) over some field \(k\), where \(A\) is a vector space over the field \(k\).