5.7. Subobjects and Quotient Objects
The entire point of category theory, contrary to its name, is to unify mathematics. Mathematicians saw the same stories over and over again in algebra and topology, and one day they got sick of it and decided to start naming the patterns they were seeing. Mathematicians achieved a level of abstraction where we no longer really care about the objects, but we want to study the morphisms between them. However, in many categories, the objects are often things like groups, rings, or topological spaces; hence there are subgroups, subrings, and spaces with subset topologies which also exist inside categories we study. This presents a challenge for category theory: how do we generalize the notion of subgroups or subspaces if we always avoid explicit reference to the elements?
It turns out that the correct way to go about this is to consider the philosophy of sub-"things": whenever \(S\) is a sub-"thing" of \(X\), there usually exists a monomorphism
For example, in Set, \(S \subset X\) implies that there's an injection \(i: S \to X\); a monomorphism is injective in Set, so this makes sense. In Top, if \(S \subset X\) where \(S\) is given the subspace topology, then the inclusion function \(i: S \to X\) is continuous, so there does exist a monomorphism \(m: S \to X\) in Top.
Thus we see that these monomorphisms give us sub-"things," and so we might naively say the set of all "subobjects" of an object \(X\) in a category \(\cc\) is the set
However, the space of all of these monomorphisms is huge, and also repetitive. For example, in Set, if we have \(X = \{1, 2, 3, 4, 5\}\), then there are all kinds of monomorphisms into \(X\):
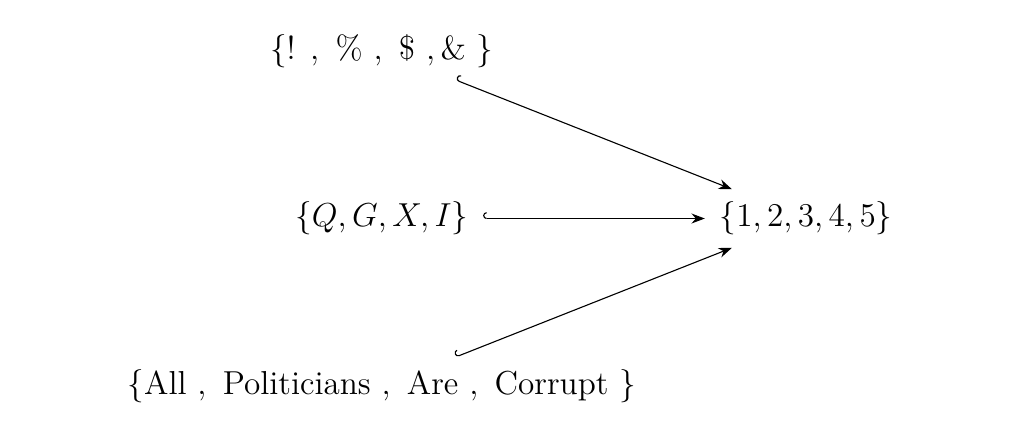Each arrow is basically saying the same thing. How do we deal with this?
Well, we can impose an equivalence relation on this space to obtain something smaller
and more manageable.
Let \(A\) an object of our category \(\cc\). Consider monomorphisms \(f: C \to A\) and \(g: D \to A\). Define the relation \(\le\) on monomorphisms of this form where \begin{statement}{ProcessBlue!10} \begin{minipage}{0.6\textwidth}
\end{minipage} \begin{minipage}{0.4\textwidth}
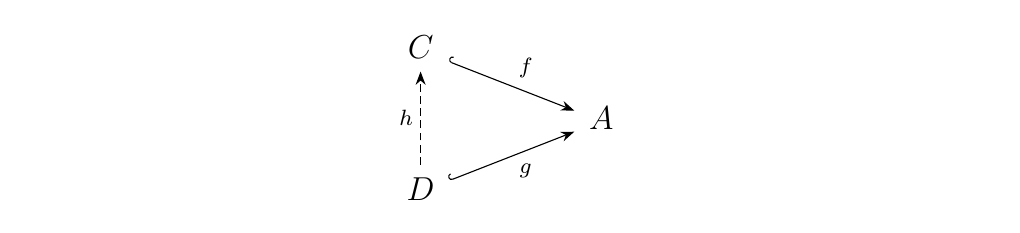
\end{minipage} \end{statement} for some monomorphism \(h: D' \to D\). Note that if \(f \le g\) and \(f \ge g\), then \(C\) and \(D\) are isomorphic (this is not true in general; this only true here because \(f, g\) are monomorphisms). So we now have our equivalence relation: we say \(f \sim g\) if there exists an isomorphism \(\phi: D \to C\) which makes the above diagram commute.
Let \(\cc\) be a category and let \(A\) be an object. We say a subobject of \(A\) is an equivalence class of monomorphisms \(f: S \to A\) under the equivalence relation \(\sim\). We denote this space of equivalence classes as
Let \(\cc\) be a category. An interesting application of subobjects occurs in functor categories. To illustrate this we consider the functor category \(**Set**^{\cc}\); that is, the category with functors \(F: \cc \to **Set**\) whose morphisms are natural transformation \(\eta: F \to G\) between such functors.
If we play around with these functors long enough, we may ask the question: What happens when, for a functor \(F: \cc \to **Set**\), there is another functor \(G: \cc \to **Set**\) such that
Could we logically call \(G\) a "subfunctor" of \(F\)? We could with a little more work. Because \(G(A) \subset F(A)\), we know that there exists a monomorphism (just an injection here) \(i_A: G(A) \to F(A)\). Now a natural question to ask here is if this translates to a natural transformation. That is, does the diagram below commute?
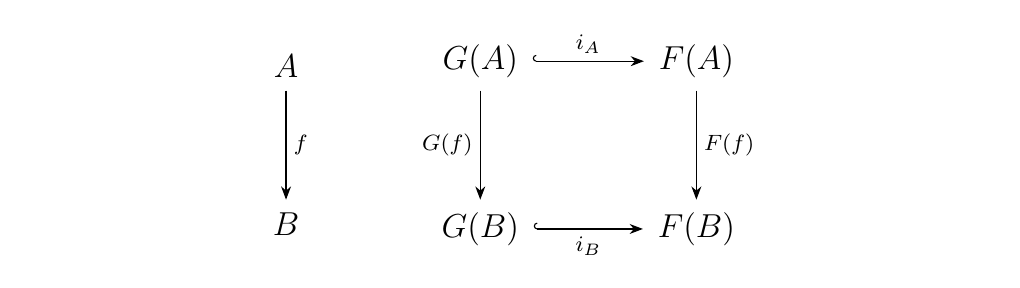
The answer is no. This is because \(G(f)\) and \(F(f)\) could be two entirely different functions which do two entirely different things to the same elements in different domains; however, one way for this diagram to commute is if \(G(f)\) is \(F(f)\) restricted to the set \(G(A)\). That is, if
The diagram then commutes. But is this the only way to make it commute? Suppose with no assumption of \(G(f)\) that the diagram did commute. Then we can still make a morphism \(F(f)\big|_{G(A)}: G(A) \to G(B)\) to get the commutative diagram
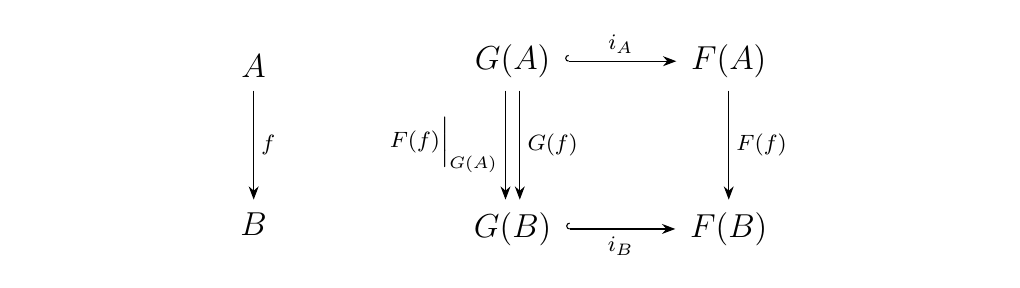
Then we see that \(i_B \circ G(f) = i_B \circ F(f)\big|_{G(A)}\). However, \(i_B\) is a monomorphism, so \(G(f) = F(f)\big|_{G(A)}\). Hence the only way to make the diagram commute is if \(G(f)\) is a restriction of \(F(f)\).
Thus we could define \(G: \cc \to **Set**\) to be a subfunctor of \(F: \cc \to **Set**\) if \(G(A) \subset F(A)\) and \(G(f: A \to B) = F(f)\big|_{G(A)}\). Or, equivalently, if \(G(A) \subset F(A)\) and that this relation is natural.
However, we can recover the same concept by applying subobjects to this functor category. In this case, we can (with laziness) say a \(G: \cc \to **Set**\) is a subobject of the functor \(F: \cc \to **Set**\) in \(**Set**^{\cc}\) if there exists a monic natural transformation \(\eta: G \to F\).
Unwrapping this definition, we see that a monic natural transformation in this case is just one where each morphism \(\eta_A: G(A) \to F(A)\) is a monomorphism, which, in our case, just means an inclusion function, such that the necessary square commutes. However, we already showed that we get the commutativity of the necessary square if and only if \(G(f: A \to B) = F(f)\big|_{G(A)}\).
Hence we have recovered the same concept of a subfunctor in two different ones; one in which we followed our intuition, and one in which we blinded applied the concept of a subobject in the functor category \(**Set**^{\cc}\).
The previous example allows us to make the definition:
Let \(\cc, \dd\) be categories. Then a functor \(G: \cc \to \dd\)
is a subfunctor of \(F: \dd \to \cc\) if \(G\) is a subobject of \(F\)
in the functor category \(\dd^{\cc}\).
Now, perhaps unsurprisingly, the entire process above can be dualized. When we dualize, however, we obtain a generalization of the concept of quotient objects. Instead of just dualizing and being boring, we'll motivate why we'd even care for such a dual concept. \
In interesting categories such as Ab or Top, we not only have subgroups and subspaces, but we also have quotient groups and quotient spaces. For the case of abelian groups, we can, for any such group \(G\), consider any subgroup \(H \le G\) and construct the quotient group \(G/H\). This comes with a a nice epimorphism \(\pi: G \to G/H\) where \(g \mapsto g + H\).
For topological spaces \((X, \tau)\) in Top, we can define an equivalence relation \(\sim\) on \(X\) and consider the topological space \((X/\sim, \tau')\) such that \(\tau'\) is the topology where a set \(U\) is open if \(\{x \mid [x] \in U\}\) is open in \(\tau\). We can then equip ourselves with a continuous projection map \(\pi: X \to X/\sim\), which is also an epimorphism.
With these few examples, we see that it is worthwhile to generalize the concept of quotient objects; to do this however requires no explicit mention of the elements of the objects of the category. However, we can maintain the philosophy seen in the previous two examples to generalize the concept.
For an object \(A\) in a category \(\cc\), we consider all epimorphisms
and call objects such objects \(Q\) as quotient objects. Again, the space of these objects is too large, so we instead consider ordering relation
\begin{statement}{ProcessBlue!10} \begin{minipage}{0.6\textwidth}
\end{minipage} \begin{minipage}{0.4\textwidth}
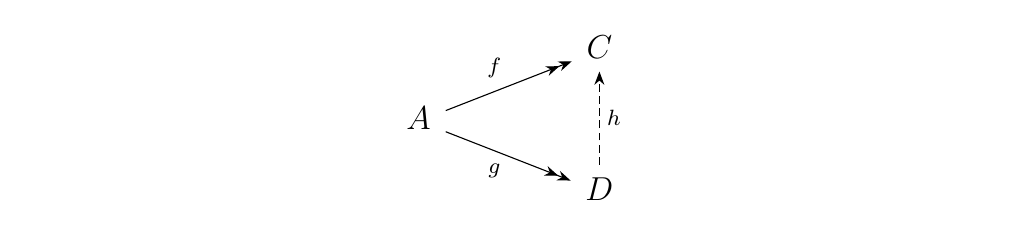
\end{minipage} \end{statement} Observing that \(f \le g\) and \(g \le f\) together imply that \(C \cong D\), we see that we may construct an equivalence relation \(\sim\) where $f \sim g $ if there exists an isomorphism \(\phi: D \to C\) such that \(f = \phi \circ g\). We can now outline a clear definition.
Let \(\cc\) be a category and let \(A\) be an object. We say a quotient object of \(A\) is an equivalence class of morphisms \(f: A \to Q\). We then denote
A quotient object in Cat is a quotient category (from chapter 2)