Skip to content

5.5. Adjoints on Limits

Consider the free monoid functor \(F\) and the forgetful functor \(U\), as below. Recall that they form an adjunction.

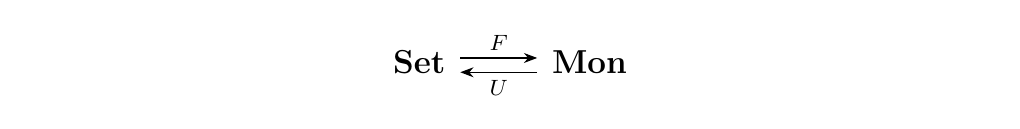The way that we philosophically interpret this adjunction is as follows: For a set \(X\), a monoid homomorphism \(\phi: F(X) \to M\) gives rise to a unique set function \(f: X \to U(M)\). Conversely, a set function \(g: X \to U(M)\) gives rise to a unique monoid homomorphism \(\psi: F(X) \to M\).

We will now observe that these functors exhibit nice behavior.

  • Recall that products in \(**Mon**\) are simply products of monoids, while products in Set are cartesian products. One can show that, for two monoids \(M\), \(N\), we have the isomorphism
\[ U(M \times N) \cong U(M) \times U(N). \]

Regarding this functor's behavior, we say that the forgetful functor \(U\) preserves products. * We may ask if the converse holds: Does the free functor preserve products? The answer is no: Given two sets \(X, Y\), it is generally not true that \(F(X \times Y) \cong F(X) \times F(Y)\) (as monoids).

An easy way to see this is to let \(X = Y = \{\bullet\}\), the one point set. Then \(F(\{\bullet\} \times \{\bullet\}) \cong F(\{\bullet\}) \cong \zz\), while \(F(\{\bullet\}) \times F(\{\bullet\}) \cong \zz \times \zz\). * What is interesting, however, is that the free functor does preserve coproducts. Recall that the coproduct in Set is the disjoint union, while the coproduct in Mon is the free product of monoids. Then it is true that, for two sets \(X, Y\),

\[ F(X \amalg Y) \cong F(X) * F(Y). \]

Thus we see that we have two functors that separately preserve products and coproducts. This is actually very interesting; after all, a very useful question to ask about a functor is if it preserves products, coproducts, equalizers, etc. For example, the fundamental group functor preserves products, and this is an interesting result one usually proves a topology course.

We now explain why we have this nice behavior.

Suppose \(G: \dd \to \cc\) is a right adjoint and \(F: \cc \to \dd\) is its left adjoint. Then \(G\) preserves limits and \(F\) preserves colimits.

Before a proof, we make some comments.

  • An easy way to remember this is RAPL: "Right Adjoints Preserve Limits." (Speaking from experience, say it in your head a bunch of times or you'll forget.) If you can remember RAPL, then you can remember that, dually, left adjoints preserve colimits.
  • The converse of this theorem does not hold.
  • Typically, this proof is shown in one of two forms: It is "blackboxed" with a slick application of the Yoneda Lemma, which is not illuminating or useful for a new reader. Or, it is more usefully spelled out by showing that right adjoints preserve limits, and the second statement is obtained by "dualizing". For variety, we will show that left adjoints preserve colimits. Then, the reader can try proving themselves that right adjoints preserve limits.

Let \((\Colim H, \sigma_i: H(i) \to \Colim H)\) be the colimit of the functor \(H: J \to \cc\). This means that we have the universal diagram below.

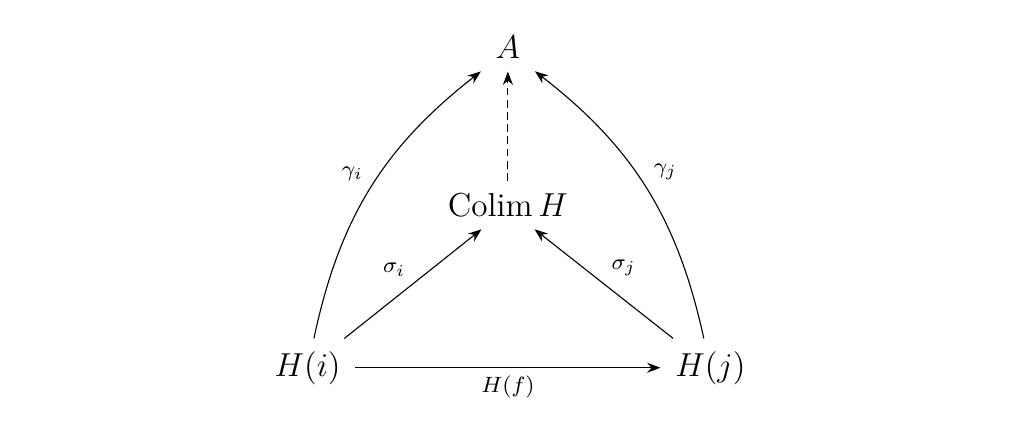
Mapping this to \(\dd\) under \(F: \cc \to \dd\), we obtain the diagram

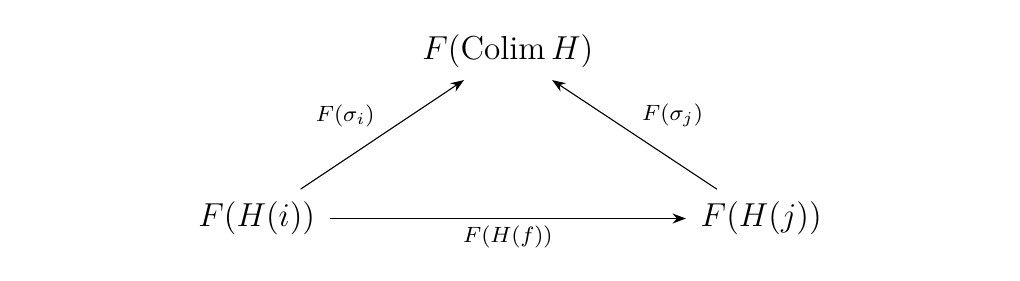
We see that \((F(\Colim H), F(\sigma_i): F(H(i)) \to F(\Colim H))\) is a cone over the functor \(F \circ H: J \to \dd\). We must show it is universal. Towards that goal, let \((C, \tau_i: F(H(i)) \to C)\) be a cone over \(F \circ H: J \to \dd\). We must show that

  • 1. There exists a \(\alpha: F(\Colim H) \to C\) such that \(\alpha \circ F(\sigma_i) = \tau_i\) for all \(i \in J\)
  • 2. \(\alpha\) is the unique morphism from \(F(\Colim H)\) to \(C\) with this property.

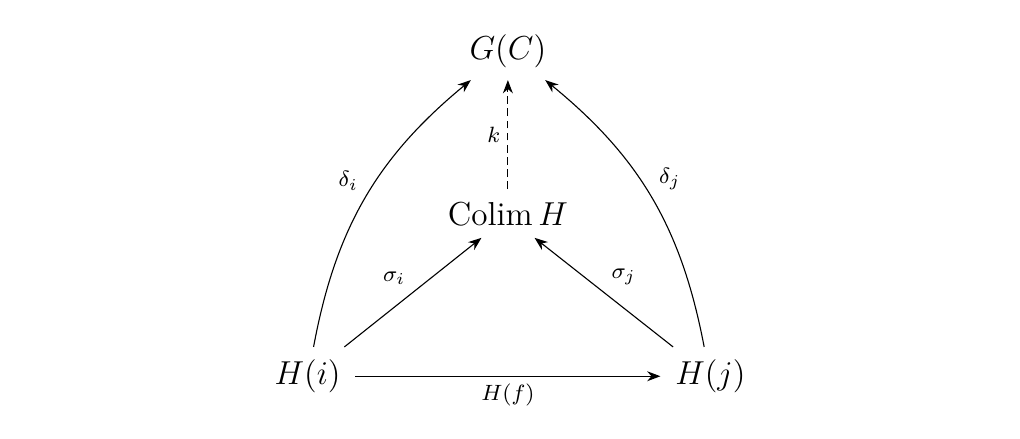
We show existence. Observe that each \(\tau_i: F(H(i)) \to C\) induces a unique morphism \(\delta_i: H(i) \to G(C)\) such that the diagram below commutes.

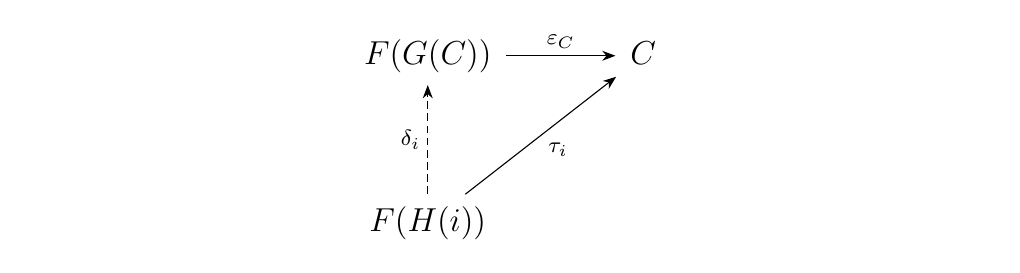Hence, we have a family of \(\delta_i: H(i) \to G(C)\). However, since \(\Colim H\) is the colimit of \(H\), we obtain a unique morphism \(k: \Colim H \to G(C)\) such that the diagram commutes.

We then map this diagram in \(\cc\) to the diagram below in \(\dd\) via \(F\):

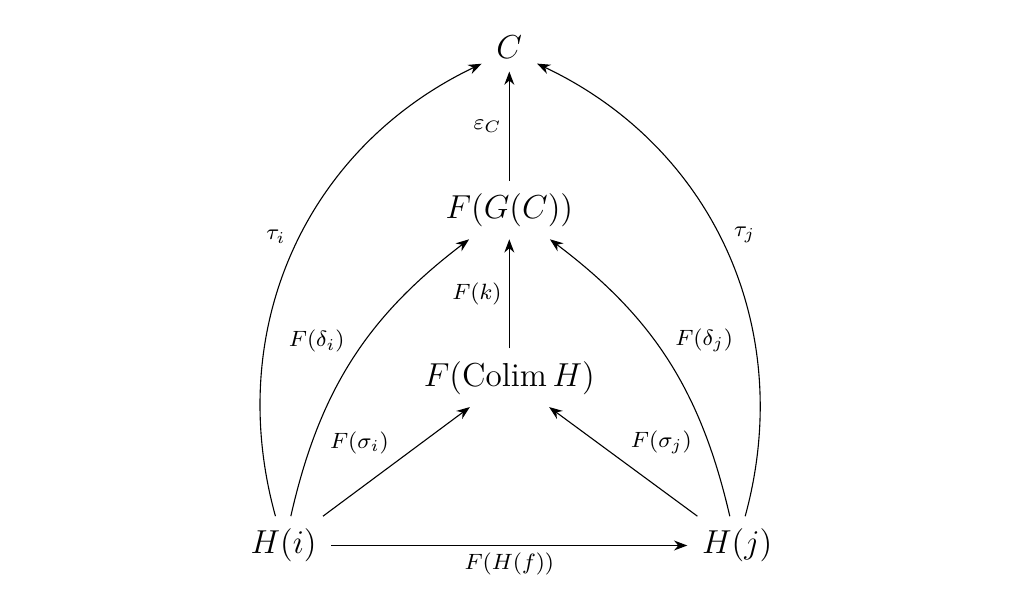
Thus we see that \(\epsilon_C \circ F(k): F(\Colim H) \to C\) is a morphism pointing from \(F(\Colim)\) to \(C\) such that the above diagram commutes. We have proved existence of such a morphism. It is not difficult to show uniqueness, which is left as an exercise. Once we have uniqueness, we can then conclude that \((F(\Colim H), F(\sigma_i): F(H(i)) \to F(\Colim H)\) forms a universal cone over \(F \circ H: J \to \dd\), so that \(F(\Colim H)\) is the colimit, as desired.

Using the above theorem, we now know that the free monoid functor \(F: **Set** \to **Mon**\) preserves coproducts. Therefore, we can say that for any sets \(X, Y\), we have that

\[ F(X \amalg Y) \cong F(X) * F(Y). \]

Moreover, the free monoid functor is part of a larger family of free functors:

  • Free group functor, \(F: **Set** \to **Grp**\)
  • Free abelian group functor, \(F: **Set** \to **Ab**\)
  • Free ring functor, \(F: **Set** \to **Ring**\)
  • Free \(R\)-module functor, \(F: **Set** \to R**-Mod**\)

who are the left adjoints to their respective forgetful functors. However, the coproduct in some of these categories is not always the free product. For example, the coproduct of \(**Grp**\) is the free product, but the coproduct in \(**Ab**\) is the direct sum. Hence, the above theorem tells us that coproducts are preserved, but to obtain the correct isomorphism, we need to remember what the coproduct in the codomain category of our left adjoint is.

Let Meas be the category of measure spaces with measure-preserving morphisms. More precisely,

  • Objects. The objects are triples \((X, \mathcal{A}, \mu_X)\) where \(X\) is a topological space, \(\mathcal{A}\) is a sigma algebra on \(X\), and \(\mu_X\) is a measure on \(X\).
  • Morphisms. A morphism between two objects \((X, \mathcal{A}, \mu_X)\) and \((Y, \mathcal{B}, \mu_Y)\) is a function \(f: X \to Y\) such that \(f\) is measurable and preserves measure. That is, is \(f\) is measurable and
\[ \mu_X(f^{-1}(B)) = \mu_Y(B) \]

for every \(B \in \mathcal{B}\).

Let \(U: **Meas** \to **Set**\) be the forgetful functor, forgetting measure space properties and measurability of the morphisms. This functor can't have a left-adjoint, since it does not preserve products. In fact, Meas cannot even have products. The main issue with this is that we cannot guarantee the projection morphisms to preserve measure. For example, if we consider the simple measure space \((\mathbb{R}, \mathcal{B}, \mu)\) where \(\mathcal{B}\) consists of the Borel algebra and \(\mu\) is the Lebesgue measure, then one reasonable way to try to form a product with itself is to construct the triple

\[ (\rr \times \rr, \mathcal{B} \times \mathcal{B}, \mu\times\mu). \]

However, observe that the projection \(\pi: (\rr \times \rr, \mathcal{B} \times \mathcal{B}, \mu\times\mu) \to (\rr, \mathcal{B}, \mu)\) is not measure preserving:

\[ \mu \times \mu(\pi^{-1}([0, 1])) = \mu \times \mu([0, 1] \times \rr) = \infty \]

while

\[ \mu([0, 1]) = 0. \]

Therefore, we cannot form products. Hence our forgetful functor has no left adjoint.

One could guess that the left adjoint would be the measure-constructing functor \(F: **Set** \to **Meas**\) where

\[ X \mapsto (X, \mathcal{P}, \mu_0) \]

where \(\mathcal{P}\) is the sigma algebra on the power set, and \(\mu_0\) assigns the measure of each set to zero (i.e. the trivial measure) but this is not the case. In fact, this functor itself also cannot have a left-adjoint because it doesn't preserve products (since Meas can't have products).

{\large Exercises \vspace{0.2cm}}

  • *1.* Denote the free monoid functor as \(F\). Prove directly that for two sets \(X\), \(Y\), we have the isomorphism of monoids \(F(X \amalg Y) \cong F(X) * F(Y)\). (Doing this is actually very important; The proof of Theorem \ref{theorem:RAPL} will become more intuitive.)
  • *2.* Finish the proof of Theorem \ref{theorem:RAPL}

  • *3.* Let \(\cc, \dd\) be categories with finite products.

    • i. Let \(F: \cc \to \dd\) be a functor that preserves products, so that for two objects \(A\), \(B\) of \(\cc\), there exists an isomorphism
    \[ F(A \times B) \cong F(A) \times F(B). \]

    Does this isomorphism have to be natural in \(A, B\)? * ii. Suppose \(F: \cc \to \dd\) is a right adjoint. Is the isomorphism \(F(A \times B) \cong F(A) \times F(B)\) natural now?