2.6. Graphs, Quivers and Free Categories
In studying category it is often helpful to imagine the objects and morphisms in action as vertices and edges corresponding to a graph. In fact, such a pictorial representation of a category is not even incorrect; one can pass categories and graphs from one to the other. To speak of this, we first review some terminology.
A (small) graph \(G\) is a set of vertices \(V(G)\) and a set edges \(E(G)\) such that there exists an assignment function
which assigns every edge to the ordered pair containing its endpoints.
On the other hand, a directed graph is a graph \(G\) where \(E(G)\) is now a set of 2-tuples \((v_1, v_2)\). This allows each edge of \(E(G)\) to have a specified direction. In this case, the assignment function has the form \(\partial: E(G) \to V(G)\). Now, how do we formulate a morphism between two graphs?
A graph homomorphism between two graphs \(G\) and \(H\) is a function \(f: G \to H\) which induces maps \(f_V: V(G) \to V(H)\) and \(f_E: E(G) \to E(H)\) where if \(\partial(e) = (v_1, v_2)\), then
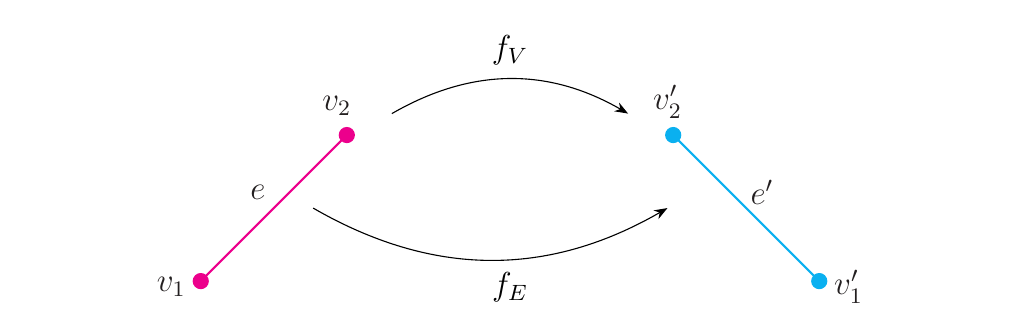
In some sense, this behaves almost like a functor. This observation will become important later. Now since we have a consistent way to speak of graphs and their morphisms, we can form the category Grph where the objects are small graphs and the morphisms are graph morphisms as described above.
Finally we introduce the concept of a quiver, which we will see is basically the skeleton of a category.
A quiver is a directed graph \(G\) which allows multiple edges between vertices. Instead of a function \(\partial\), a quiver is equipped with source and target functions
So a quiver is a 4-tuple \((E(G), V(G), s, t)\). Now as before, a morphism \(f: Q \to Q'\) between quivers \((E(Q), V(Q), s, t)\) and \((E(Q'), V(Q'), s', t')\) is one which preserves edge-vertex relations. Thus, it is a pair of functions \(f_E: E(Q) \to E(Q')\) and \(f_V: V(Q) \to V(Q)'\) such that
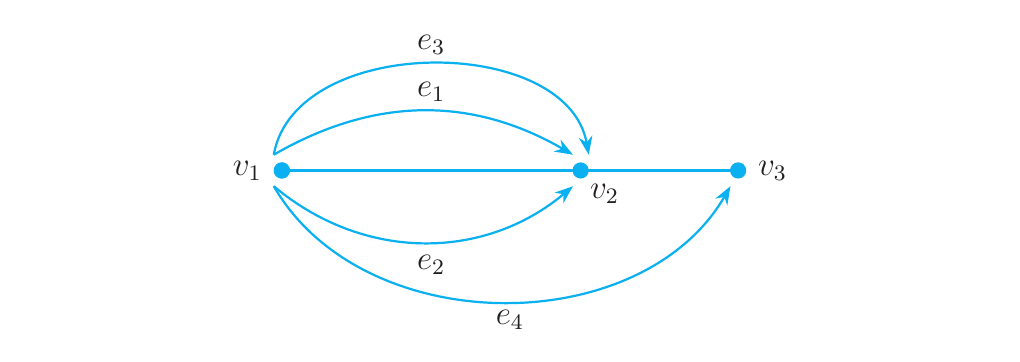
\noindent Now that we have all of those definitions out of the way, what's really going on here? A quiver can be abstracted as a pair of objects and morphisms.
If we let \(C\op\) be the category with two objects, two nontrivial morphisms
and two identity morphisms as below
then we see that a quiver is a functor \(F: \cc\op \to **Set**\).
With that said,
we can define the category of quivers Quiv, which, based on what we just showed,
is a functor category with objects \(F: \cc\op \to **Set**\). This
allows us to interpret quiver homomorphisms as natural transformations.
\textcolor{MidnightBlue}{Now why on earth do we care about these things called quivers?} The reason is because the underlying structure of small categories take the form of a quiver. For example, the category on the left below can be turned into a quiver, as on the right, after "forgetting" composition and identity morphisms.
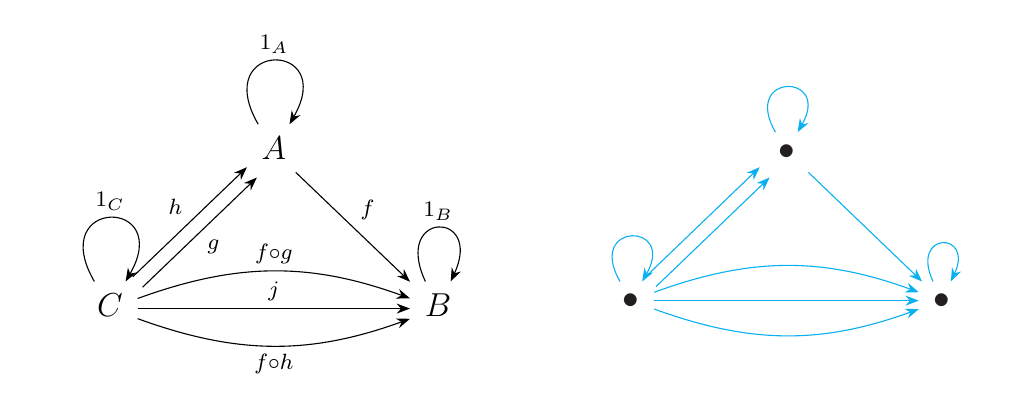
In general, since categories allow multiple arrows between objects, we can construct a forgetful functor which forgets composition and identity arrows.
Note that if \(F : \cc \to \cc'\) is a functor then \(U(F) : U(\cc) \to U(\cc')\) is in fact a well-behaved morphism between two quivers. \textcolor{NavyBlue}{Recall that the construction of a graph homomorphism is basically a functor as we've known to so far}.
Not only can we forget categories to generate quivers, we can generate categories using the skeletal structure of a quiver. This leads to the concept of a free category; the concept is no different than the concept of, say, a free group generated by a set \(X\).
Let \(Q\) be a quiver with vertex set \(V\) and edge set \(E\). We define the free category generated by \(Q\) as the category with
- Objects. The set \(V\)
- Morphisms. The paths of the quiver.
Precisely, a path is any sequence of edges and vertices
with composition of paths defined in the intuitive way:
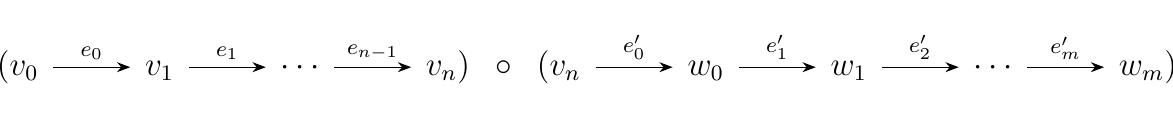
When we generate the free category, we also remember to add identity arrows to
each vertex.
Since for each quiver \(Q\), we can define a free category \(F_C(Q)\) on \(Q\), we can realize that this mapping is functorial. That is, we can define a functor
where it maps on objects and morphisms as \begin{statement}{Red!10}
\end{statement} That is, quiver homomorphisms can map to functors \(F_C(f)\) between the free categories generated by the respective quivers.
Now, what is the relationship between a quiver \(Q\) and the quiver \(U(F_C(Q))\)? There must exist an injection \(i: Q \to U(F(Q))\) which sends \(Q\) to the skeleton of \(U(F_C(Q))\). It turns out that this morphism is universal from \(Q\) to \(U\).
Let \(Q\) be a quiver. Then there is a graph homomorphism \(i: Q \to U(F_C(Q))\) such that, for any other graph homomorphism \(\phi: Q \to U(\cc)\) with \(\cc\) a category, there exists a unique functor \(F: F_C(Q) \to \cc\) where \(U(F) \circ i = \phi\). That is,
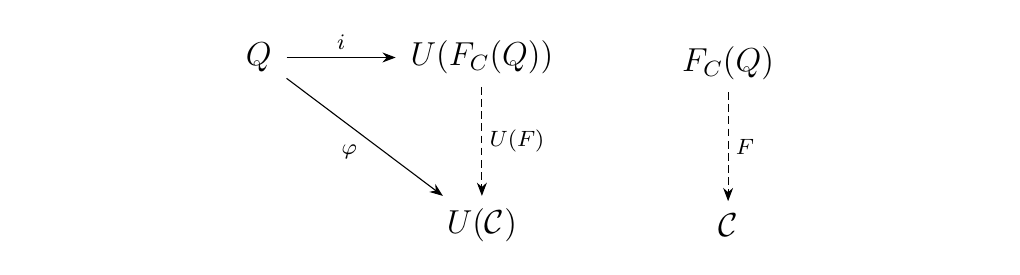
This is an example of a universal arrow; the dotted lines are the morphisms which are forced to exist by the conditions of the diagram, which is the idea of a universal element.
Denote each morphism or path in \(F_C(Q)\) of length \(n\)
as \((v_0, e_0e_1\cdots e_{n-1}, v_n): v_0 \to v_n\). Now define the inclusion
\(i: Q \to U(F_C(Q))\) where each vertex and edge is sent identically. That is, vertices
\(v\) map to \(v\) in \(F_C(Q)\), and morphisms are sent identically and for each
edge \(e: v \to v'\):
An important observation to make is the fact that every morphism \((v_0, e_0e_1\cdots e_{n-1}, v_n): v_0 \to v_n)\) in \(F_C(Q)\) is a composition of length 2-morphism:
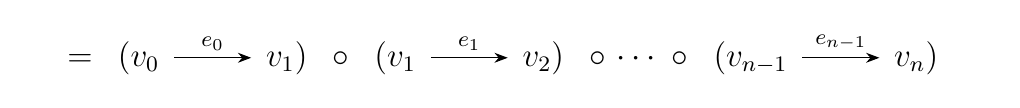Therefore, for any graph homomorphism \(\phi: Q \to U(\cc)\),
we can create a unique functor \(F: F_C(Q) \to \cc\) where
which then gives us
as desired.