2.3. Functor Categories
In the proof for the last proposition, we used a trick of forming a desired natural transformation by composing two composable natural transformations. Hence, we see that natural transformations can be "composed." We refine this notion as follows.
Let \(\cc\) and \(\dd\) be categories and consider three functors \(F, G, H: \cc \to \dd\). Suppose further that we have two natural transformations \(\sigma, \tau\) as below:
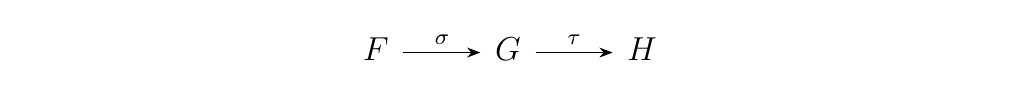(This might seem like a weird way to write this, but we are trying to hint at something.)
Using these two natural transformations,
we can define a natural transformation
where, for each \(C \in \cc\), we define
Visually, we can picture what we are doing as follows. For a given morphism \(f: A \to B\) in \(\cc\), we define the morphism \((\tau \cdot \sigma)_C\) as
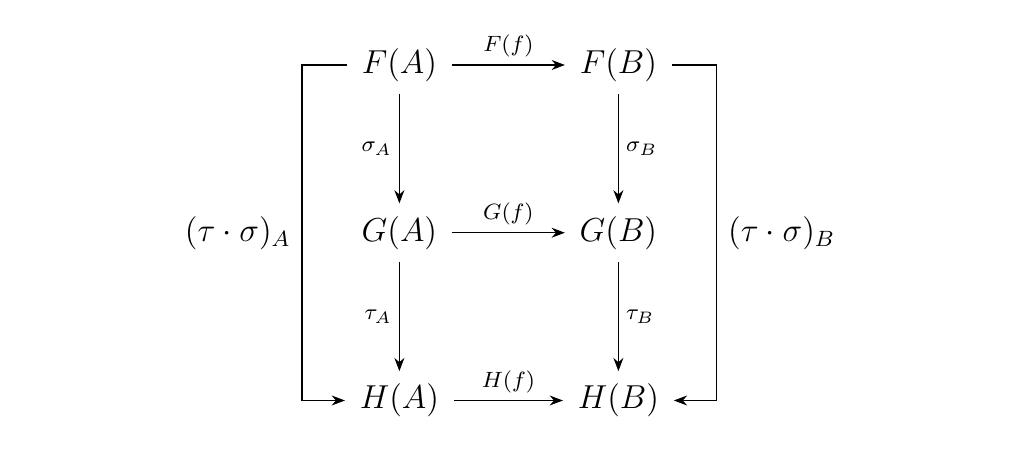Thus, we see that natural transformations can be "composed,"
and we can thus ask: If we view functors as objects, and view natural transformations
as morphisms, do we get a category? The answer is yes.
Let \(\cc\) and \(\dd\) be small categories and consider set of all functors \(F: \cc \to \dd\). Then the functor category, denoted as \(\dd^\cc\) or \(\fun(\cc, \dd)\), is the category where
- Objects. Functors \(F: \cc \to \dd\)
- Morphisms. Natural transformations \(\eta: F \to G\)
Functor categories are extremely useful, as we shall see that they're the categorical version of representations.
When we think of representations, we usually think of a group homomorphism \(\rho: G \to \text{GL}_n(V)\) for some vector space \(V\) over a field \(k\). However, suppose we wanted to be a real smart-ass and say "Well, can't we regard \(\rho\) as actually a functor between two one-object categories whose morphisms are all isomorphism?" The answer is yes!
What this then means is that the category of representations of a group \(G\) is actually a functor category. Specifically,
Hence in some cases it helps to think of \(\fun(\cc, \dd)\) as a category of representations of \(\cc\). This makes sense, since that is really what a functor is. A functor preserves composition; and if we stop thinking like the set theorists, we can realize that composition controls a great deal of structure in a category \(\cc\). Hence a functor \(F: \cc \to \dd\) ``represents"" that structure in a category \(\dd\).
Let \(\bm{1}\) be the one element category with a single identity arrow. Then for any category \(\cc\), the functor category \(\cc^{\bm{1}}\) is isomorphic to \(\cc\). This is because each functor \(F: \bm{1} \to \cc\) simply associates the element \(1 \in \bm{1}\) to an element \(C \in \cc\), and the identity \(1_1: 1 \to 1\) to the identity morphism \(1_C\) in \(\cc\).
Let \(\bm{2}\) be the category consisting of two elements, containing the two identities and one nontrivial morphism between the objects.
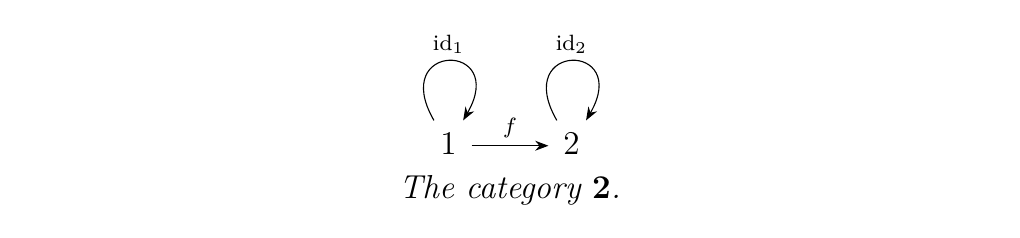Now consider the functor category \(\cc^{\bm{2}}\) where \(\cc\) is
any category. Each functor \(F:\bm{2} \to \cc\) maps the pair of
objects to objects \(F(1)\) and \(F(2)\) in \(\cc\). However, since
functors preserve morphisms, we see that
This is what each \(F \in \cc^{\bm{2}}\) does. Hence, every morphism \(g \in \hom(\cc)\) corresponds to an element in \(\cc^{\bm{2}}\). Hence, we call \(\cc^{\bm{2}}\) the category of arrows of \(\cc\).
Let \(g: C \to C'\) be any morphism between objects \(C, C'\) in \(\cc\). Construct the element \(G \in \cc^{\bm{2}}\) as follows: \(G(1) = C\), \(G(2) = C'\) and \(G(f) : G(1) \to G(2) = g\). Hence, \(\hom(\cc)\) and \(\cc^{\bm{2}}\) are isomorphic. Moreover, \(\hom(\cc)\) determines the members of \(\cc^{\bm{2}}\).
A crude way to visualize this proof is imaging \(1 \to 2\) is a "stick" with 1 and 2 on either end, and so the action of any functor is simply taking the stick and applying it to anywhere on the direct graph generated by the category \(\cc\). Hence, this is why we say \(\hom(\cc)\) determines the functor category \(\cc^{\bm{2}}\).
Let \(X\) be a set. Hence, it is a discrete category, which if recall, it's objects are elements of \(X\) and the morphisms are just identity morphisms.
Now consider \(\{0, 1\}^X\), the category of functors \(F: X \to \{0, 1\}\). Then every functor assigns each element of \(x \in X\) to either \(0\) or \(1\), and assigns the morphism \(1_x: x \to x\) to either \(1_0: 0\to 0\) or \(1_1: 1 \to 1\).
One way to view this is to consider \(\mathcal{P}(X)\), and for each \(S \in \mathcal{P}\), assign \(x\) to \(1\) if \(x \in S\) or \(x\) to \(0\) if \(x \not\in S\). All of these mappings may be described by elements of \(\mathcal{P}\), but we can also realize that each of these mappings correspond to the functors in \(\{0, 1\}^X\). Hence, we see that \(\{0, 1\}^X\) is isomorphic to \(\mathcal{P}(X)\).
Recall from Example \ref{group_ring_functors} that, given a group \(G\) and a ring \(R\) (with identity), we can create a group ring \(R[G]\) with identity, in a functorial way, establishing a functor
However, we then noticed that the above functor establishes a process where we send rings \(R\) to functors \(R[-]: **Grp** \to **Ring**\). It turns out that this process is itself a functor, and we now have the appropriate language to describe it:
Specifically, let \(\psi: R \to S\) be a ring homomorphism. Now observe that \(\psi\) induces another ring homomorphism
As a result, we see that such a ring homomorphism induces a natural transformation. To show this, let \(\phi: G \to H\) be a group homomorphism. Then observe that we get the diagram in the middle.
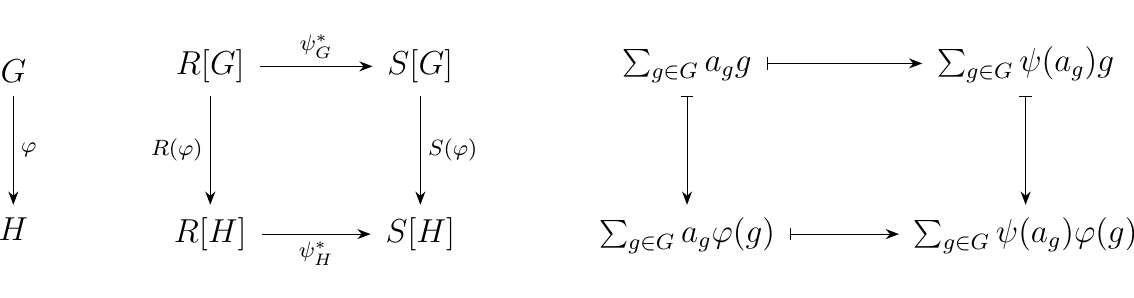However, we can follow the elements as in the diagram on the right, which shows
us that the diagram commutes. Hence we see that \(\psi^*\) is a natural transformation
between functors \(R[-] \to S[-]\). Overall, this establishes that we do in fact have
a functor
which we wouldn't be able to describe without otherwise introducing the notion of a functor category.
Let \(M\) be a monoid category (one object) and consider the functor category \(**Set**^M\). The objects of Set\(^M\) are functors \(F: M \to **Set**\), each of which have the following data:
where \(f: M \to M\) is an morphism in \(M\). Now if we interpret \(\circ\) as the binary relation equipped on \(M\), we see that for any \(g : M \to M\),
by functorial properties. Hence, each functor \(F\) maps \(M\) to a set \(X\) which induces the operation of \(M\) on \(X\). Therefore the objects of Set\(^M\) are other monoids \(X\) in Set equipped with the same operation as \(M\) and as well as the morphisms between such monoids.