1.10. Monic, Epics, and Isomorphisms

In category theory the ultimate focus is placed on the morphisms within a category. What we really care about are the relationships between the objects. Thus in this section we'll go over types of morphisms that exist between objects.

The way that this is done in set theory is to consider injective functions, surjective functions, and isomorphisms. This can also be done in topology, and in group, ring, and module theory. However, these concepts make no sense in general. This is because in general, the morphisms of a category are not functions because in general, the objects of a category are not sets (even if the objects are sets, the morphisms can still be different than functions).

We can nevertheless abstract the concept of injections and surjections by expressing their properties categorically; that is, without reference to specific elements in any objects. This leads to the concepts of monomorphisms and epimorphisms. \vspace{0.3cm}

\begin{minipage}{0.8\textwidth}

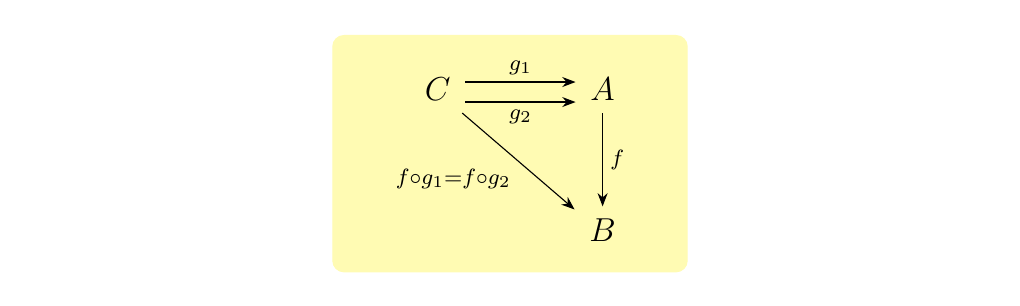
Let $f: A \to B$ be a morphism. Then

1. $f$ is a monomorphism (or is monic) if

\[ f \circ g_1 = f \circ g_2 \implies g_1 = g_2 \]

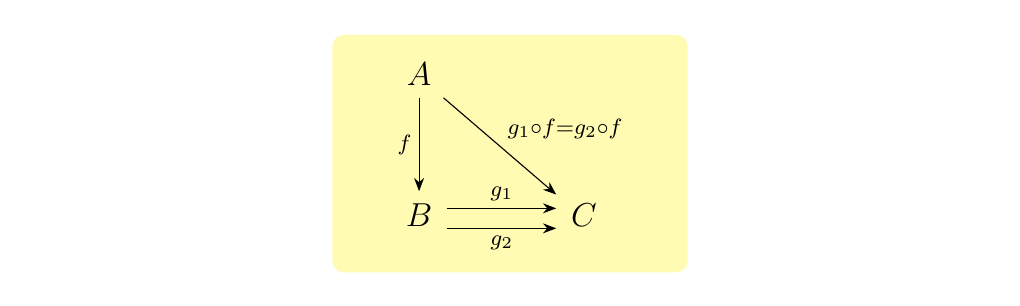
for all $g_1,g_2 : C \to A$, where $D$ is arbitrary. * 2. $f$ is a epimorphism (or is epic) if

\[ g_1 \circ f = g_2 \circ f \implies g_1 = g_2 \]

for all $g_1, g_2 : B \to C$, where $C$ is an arbitrary object. * 3. $f $ is a split monomorphism (or retraction) if, for some\ $g: B \to A$,

$$ f \circ g = 1_B.
$$ * 4. $f $ is a split epimorphism (or section) if, for some $g: B \to A$,

\[ g \circ f = 1_A. \]

\end{minipage} \hspace{-2cm} \begin{minipage}{0.1\textwidth} \vspace{-2.2cm}

\vspace{0.2cm}

\end{minipage} \vspace{1cm}

Monomorphisms and epimorphisms are an abstraction that take advantage key properties of both injective and surjective functions. We illustrate this with a few examples.

In $\Set$, an injective function $f: X \to Y$ is "one-to-one" in the sense that $f(x) = f(y)$ if and only if $x = y$. With that said, suppose that $g_1, g_2: Z \to X$ are functions and moreover that $f\circ g_1 = f \circ g_2$. Then this means that, for all $z \in Z$, we have that

\[ f(g_1(z)) = f(g_2(z)) \implies g_1(z) = g_2(z) \]

since $f$ is one-to-one. Hence we see that injective functions are monomorphisms in $\Set$; one can then conversely show that a monomorphism in $\Set$ are injective functions.

Let $(G, \cdot)$ be a group, and suppose $(H, \cdot)$ is a normal subgroup of $G$. Then with such a construction, we always have access to the inclusion and projection homomorphisms

\[\begin{align*} i: H \to G \qquad &i(h) = h \\ \pi: G \to G/H \qquad &\pi(g) = g + H. \end{align*}\]

It is not hard to see that $i$ is a monomorphism and $\pi$ is an epimorphism; for suppose $\phi, \psi:K \to G$ are two group homomorphisms from some group $K$ where $i \circ \phi = i \circ \psi$. Then for each $k \in K$, $i(\phi(k)) = i(\psi(k)) \implies \phi(k) = \psi(k)$, so that $\phi = \psi$. Conversely, if $\sigma, \tau: G \to M$ are two group homomorphisms to some group $M$ such that $\sigma \circ \pi = \tau \circ \pi$, then because $\pi$ is surjective we have that $\sigma = \tau$. Hence, we see $\pi$ is an epimorphism.

Since the above constructions can be repeated in the categories $\ab$, $\ring$, and $R\rmod$, so can the above argument. We'll see more generally the deeper reason for why this is the case later on.

In the category of fields, $\fld$, every nonzero morphism is a monomorphism. This is due to the classic argument: the only nontrivial ideal of a field $k$ its itself; hence the kernal of any map $\phi: k \to k'$ is either trivial or all of $k$. If we suppose $\phi$ is nonzero, then we see that it must be injective, and hence a monomorphism.

Let $f: A \to B$ be a morphism between two objects $A$ and $B$. We say that $f$ is an isomorphism if there exists a morphism $f^{-1}:B \to A$ in $\cc$! such that

\[ f \circ f^{-1} =\id_A \quad \quad f^{-1} \circ f = \id_B. \]

In this case, $f^{-1}$ is unique, and for any two isomorphisms $f:A \to B$ and $g:B \to C$ we have

\[ (g \circ f)^{-1} = f^{-1}\circ g^{-1}. \]

In this case we say that $A$ and $B$ are isomorphic and denote this as $A \cong B$.

This is a generalization of the familiar concept of isomorphisms in abstract algebra and in set theory that one usually encounters.

Next, we illustrate a few properties of these types of morphisms.

Let $F: \cc \to \dd$ be a functor. Then if $f: A \to B \in \cc$

is an isomorphism, then $F(f)$ is an isomorphism in $\dd$.
is a split monomorphism, then $F(f)$ is a split monomorphism in $F(f)$
is a split epimorphism, then $F(f)$ is a split epimorphism.

That is, functors preserve isomorphisms, split monomorphism, and split epimorphisms.
In general, functors do not reflect isomorphisms, split monomorphisms, and split epimorphisms. That is, if $F(f): F(A) \to F(B)$ is an isomorphism it is not the case that $f$ is an isomorphism.

We demonstrate this with the following example.

Recall that $\text{Spec}(-): \cring \to \Set$ is a functor that appears in algebraic geometry. It sends every commutative ring $A$ to its ring spectrum $\spec(A)$, which consists of all prime ideals of $A$.

Let $\displaystyle N =\bigcap_{P \in \spec(A)}P$ be the intersection of all prime ideals. An equivalent way to speak of $N$ is the set $N = \{a \in A \mid a^m =0 \text{ for some positive integer }m\}$; that is, $N$ is equivalently the nilradical elements of $A$.

Now the projection ring homomorphism

\[ \phi: A \to A/N \]

is certainly not an isomorphism (unless $A$ has no nontrivial nilradical elements), but the image of this map under $\spec$

\[ \spec(\phi): \spec(A/N) \isomarrow \spec(A) \]

is always an isomorphism. In fact, if we impose the Zarisky topology on these prime spectrums, the functor becomes one which goes to topological spaces

\[ \text{Spec}(-): \cring \to \top \]

and the map $\phi$ becomes a homeomorphism. Hence, this functor does not reflect isomorphisms in either the set or topological senses, because the image $\spec(\phi)$ is an isomorphism, but $\phi$ is not.
Despite this,
the interpretation of this result is a useful one because it demonstrates that algebraic geometrists can "throw away" their nilradical elements without changing their Zariski topology.

The composition of monomorphisms (epimorphisms) is a (an) monomorphism (epimorphism).

Let $f: A \to B$ and $g: B \to C$ be monomorphisms, and suppose $h_1, h_2 : D \to A$ are two parallel morphisms. Suppose that $(g \circ f) \circ h_1 = (g \circ f) \circ h_2.$ Note that we can rewrite the equation to obtain that

\[ g \circ (f \circ h_1) = g \circ (g \circ h_1) \implies f \circ h_1 = f \circ h_2. \]

as $g$ is monic, and hence it is left cancellable. But once again, $f$ is monic, so we cancel on the left to obtain that $h_1 = h_2$ as desired.

\textcolor{MidnightBlue}{Note: it is not always the case that a monic, epic morphism is an isomorphism (that is, it's not always invertible.)}

Consider the category $\top$, consisting of (small) topological spaces as our objects with continuous functions between them as morphisms. Let $D$ be a dense subset of a topological space $X$ and let $i: D \to X$ be the inclusion map. We'll show that this function is both epic and monic.

To show it is epic, let $f_1, f_2: X \to Y$ be continuous maps form $X$ to another topological space $Y$. Let $Y$ be Hausdorff, and suppose that

\[ f_1 \circ i = f_2 \circ i. \]

Now $\im(i) = D$, so the above equation tells us that $f_1(d) = f_2(d)$ for all $d \in D$. That is, the functions agree on the dense subset. However, we know from topology that this implies that $f_1 = f_2$.

\textcolor{MidnightBlue}{ Suppose that $f_1(x) \ne f_2(x)$ for some $x \notin D$. Since the points are distinct, and since $Y$ is Hausdorff, there must exist disjoint open sets $U, V$ in $Y$ such that $f_1(x) \in U$ and $f_2(x) \in V$. Since both $f_1, f_2$ are continuous, there must exist open sets $U', V'$ in $X$ such that $f(U') \subset U$ and $g(V') \subset V$. \ \indent However, since $D$ is dense in $X$, both $U'$ and $V'$ must intersect with some portion of $D$; that is, there is some $y \in U'$ and $z \in V'$ such that $y, z \in D$. Therefore, we see that $f_1(y) \in U$ and $f_2(z) \in V$, and since $y, z \in D$ we have that $f_1(y) = f_2(z)$. But this contradicts the fact that $U \cap V = \emptyset.$ Therefore, we have a contradiction and it must be the case that $f_1(x) = f_2(x)$ for all $x \in X$, as desired. } \noindent Therefore, we see that $i$ is epic. To show that it is monic, suppose $g_1, g_2: Y \to D$ are two parallel, continuous functions, and that

\[ i \circ g_1 = i \circ g_2. \]

Since $i$ is nothing more than an inclusion map, we immediately have that $g_1 = g_2$. Therefore, $i$ is also monic.

However, note that $i: D \to X$ is not an isomorphism, since it is not necesasrily always surjective. Hence $i$ is an example of a monic, epic morphism which is not an isomorphism.

We finish our discussion on monics and epics by considerig the automorphism groups of a category.

Let $\cc$ be a locally small category. For each object $A$ in $\cc$, we can consider the automorphism group $\aut(A)$ whose objects consist of isomorphisms $\phi: A \isomarrow A$, whose product is composition, and whose identity is $1_A$.

Note that despite the notation, this does not generally define a functor.

Some examples of the above construction include familiar and useful examples in mathematics.

For any group $(G, \cdot)$ in $\grp$, we can formulate the automorphism group $\aut(G)$ which is the group of isomorphisms from $G$ to itself. Depending on $G$, this can have all kinds of behavior. For example, if $\aut(G)$ is cyclic, then $G$ is abelian. If $G$ is an abelian group of order $p^n$, then $\aut(G) = GL(n, F)$ where $F$ is the finite field of order $p$.
For any set $X$ in $\Set$, the automorphism group $\aut(X)$ consists of the bijections on $X$ to itself; by definition in set theory, these are just permutations. Hence the automorphism group is the permutation group of the elements of $X$.
For any field $(k, \cdot, +)$ in $\fld$, the automorphism group $\aut(k)$ also consists of field isomorphisms to itself. In this setting, what is often of more interest is considering the subgroups of $\aut(k)$, often denoted as $\aut(k/L)$, which are automorphisms that fix the subfield $L$. These subgroups are key to studying polynomial roots and hence are prevalent in Galois theory.
For any graph $(G, E, V)$ in Grph, one can construct the automorphism group $\aut(G)$, which tracks the symmetries of the graph. Interestingly, there is a theorem known as Frucht's Theorem which states that every finite group is the automorphism group of a finite (undirected) graph; this was later extended and shown that every group is the automorphism group of a directed graph [Groups represented by homeomorphism groups.].
For any topological space $(X, \tau)$ in $\top$, the autormorphism group $\aut(X)$ consists of the homeomorphisms to itself. Geometrically, these record the possible ways of continuously deforming a space back into itself. It is a theorem that every group is the automorphism group of some complete, connected, locally connected metric space $M$ of any dimension.

With the automorphism group in mind, we might ask the same question on the object level: Given an object $A$ in $\cc$, what objects are isomorphic to $A$ in $\cc$? To answer this, we define the relation $\sim$ on $\ob(\cc)$, the objects of $\cc$, where we say

\[ A \sim B \text{ if } A \cong B. \]

Such an equivalence relation divides the objects of $\cc$ into disjoint isomorphsm classes, which reduces the structure of $\cc$.

Let $\cc$ be a category and $A$ any object. We call the equivalence class of $A$ under $\sim$, defined previously, as the isomorphism class which we denote as

\[ \text{Isom}(A) = \{X \in \ob(\cc) \mid X \cong A\}. \]

This leads to the following categorical construction which preserves a great deal of information within the category.

Let $\cc$ be a category, and assume the axiom of choice. Then we can construct a skeleton of a category $\cc$, denoted $\text{sk}(\cc)$, as the category where

Objects. For each $A \in \cc$, we select one representative of each isomorphism class $\text{Isom}(A)$.
Morphisms. For two representatives of isomorphism classes $A, B$, we take

\[ \hom_{\text{sk}(\cc)}(A,B)= \hom_{\cc}(A,B) \]

We note three things regarding this construction.

(1) We used the axiom of choice to build the objects of the category, since we needed to select one element from each isomorphism class.
(2) The category $\text{sk}(\cc)$ is a full subcategory of $\cc$ by definition.
(3) We note that this construction builds a skeleton. In general, a category will have different skeletons because there are many ways to construct the objects of such a skeleton.

As noted, a category will have different skeletons. However, up to isomorphism, it does not really matter which skeleton we build as we will see.

Let $\cc$ be a category, and let $\text{sk}(\cc)$ and $\text{sk}'(\cc)$ be two skeletons built from $\cc$. Then $\text{sk}(\cc) \cong \text{sk}'(\cc)$.

The prove is left as an exercise for the reader. We will see late that there are more enjoyable properties of "skeletal" categories, which we define as categories exhibiting this type of behavior.

A category $\cc$ is called skeletal if no two distinct objects are isomorphic in $\cc$.

Categorical skeletons are inadvertently studied everywhere in mathematics. For example, asking for a classification of abelian groups, of manifolds, or even of the cardinality of every set is the same thing as asking for the skeletons of $\ab$, $**DMan**$, and $\Set$. We give a few examples.

Consider the category $**FinCard**$ (read: "finite cardinals") which we describe as

Objects. The set $\varnothing$ and the sets $\{1, 2, ..., n\}$ for each $n \in \mathbb{N}$.
Morphisms. All functions between these finite sets.

Clearly this is a full subcategory of $\finset$. Moreover, it is skeletal; no two sets are isomorphic because each object is of different size. Therefore, it is skeletal. In fact, $**FinCard**$ is a skeleton of $\finset$ because any finite set (in some universe $U$) can be ordered in some way, which provides an enumeration on its objects. In other words, every finite set is of some finite size, making it isomorphic to some set $\{0, 1, 2, \dots, n\}$.

One can try to generalize the previous example to $\Set$, but this is in general not possible unless we assume ZFC with the generalized continuum hypothesis, as such a posulate is independent of ZFC.

Assuming such an axiom, we can construct the category $**Card**$ where

Objects. The sets $\varnothing, \{1, 2, \dots, n\}$ for each $n \in \mathbb{N}$, and $\omega_0, \omega_1, \omega_2, \dots$
Morphisms. All functions between such sets.

Here we see that this is again a skeleton $\Set$, since by our assumptions (which is assuming a lot), any set is of some cardinality $1, 2, \dots, n, \dots, \aleph_0, \aleph_1, \dots$. However, for each such cardinal we have a corresponding set with that cardinality. Hence each element in $\Set$ is isomorphic to some element of $**Card**$. Overall, we see that Card forms a skeleton of $\Set$.

The above example can be repeated for Cycl, the category of cyclic groups. This is because any two cyclic groups of the same order are isomorphic. Hence, one can find a skeleton of Cycl by finding a family of cylic groups of every set size (again, using the generalized continuum hypothesis).

Consider the category $**Ecld**$ of Euclidean spaces, which we may describe as

Objects. The vector spaces $\rr^n$ for each $n = 0, 1, 2, \dots, $
Morphisms. Linear transformations between vector spaces.

Then we see that $**Ecld**$ is the skeleton of $**FinVect**_k$, which is the category of finite-dimensional vector spaces. The reason why this works is because every finite dimensional vector space is isomorphic to $\rr^n$ for some $n$.

{\large Exercises \vspace{0.5cm}}

*1.* Prove Lemma \ref{lemma:composition_of_epis} for epimorphisms.
*2.* Prove Lemma \ref{lemma:skeletons_are_isomorphic}.
*3.* Describe the monomorphisms and epimorphisms in the category of $\cat$.\footnote{Classifying epimorphisms in $\cat$ is actually nontrivial, although not impossible. However, the task here is to just interpret the definition of monics and epics $\cat$. }
*4. In the category of $\ring$, give an example of a morphism which is both a monomorphism and epimorphism, but not an isomorphism. \ (Hint:* Consider the inclusion $i: \zz \to \qq$.)
*5.* Recall from Exercise ? that, in any category, if we have two commutative diagrams, we can always stack them together to obtain a larger commutative diagram. We saw, however, that converse is not always true: subdividing a commutative diagram does not produce smaller commutative diagrams.

Prove that the converse is true when all morphisms are isomorphisms.