Skip to content

4.2. Reflective Subcategories.

Let \(\aa\) be a full subcategory of \(\cc\). We say \(\aa\) is reflective in \(\cc\) whenever the inclusion functor \(I: \aa \to \cc\) has a left adjoint \(F: \cc \to \aa\). We then say the functor \(F\) is the reflector, and the adjunction \((F, I, \phi)\) is a reflection of \(B\). In the case of a reflection, we obtain the bijection of hom-sets

\[ \hom_{\aa}(F(C),A) \cong \hom_{\cc}(C, I(A)) \implies \hom_{\aa}(F(C),A) \cong \hom_{\cc}(C, A) \]

which is natural in both \(C\) and \(A\).

Let \(F: **Grp** \to **Ab**\) be the abelianization functor, which sends a group \(G\) to its free abelian group \(G/[G,G]\). From Exercise \ref{exercise:abelianization_functor_is_left_adjoint}, we know that this is left adjoint to the forgetful functor \(U: **Ab** \to **Grp**\).

However, the functor \(U: **Ab** \to **Grp**\) is isomorphic to the inclusion functor \(I: **Ab** \to **Grp**\). Hence, \(F\) is also left adjoint to the inclusion functor, so that Ab is a reflective subcategory of Grp.

Let \(**Top**\) be the category of topological spaces with morphisms continuous functions. Let \(**CHaus**\), the category of compact Hausdorff spaces, which is a subcategory of \(**Top**\).

If we let \(X\) be a topological space, then we denote \(\beta(X)\) to be the Stone-Cech compactification. Let \(I : **CHaus** \to **Top**\) be the inclusion functor. Then the definition of the Stone-Cech compactification of a space \(X\) is the universal property:

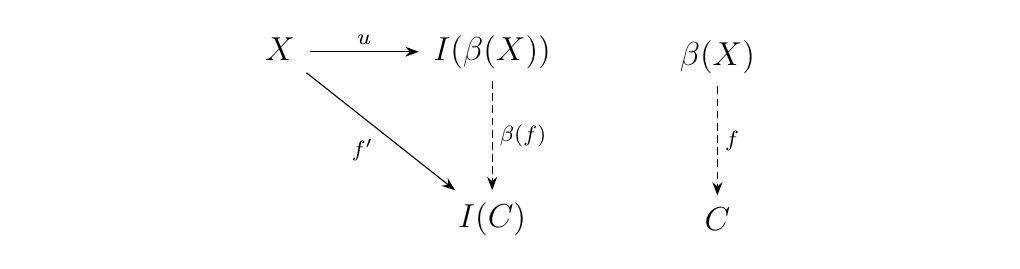That is, the Stone-Cech compactification is a topological space \(\beta(X)\) with a morphism \(u: X \to \beta(X)\) which is universal across all morphisms \(f: X \to C\) where \(C\) is compact, Hausdorff.

Thus we see that a Stone-Cech compactification gives rise to an object \(\beta(X) \in **CHaus**\) and a universal morphism \(X \to I(\beta(X))\) from \(X\) to \(I\). Now by Proposition 4.1, this makes \(\beta : **Top** \to **CHaus**\) a functor, which is left adjoint to the inclusion functor \(I: **CHaus** \to **Top**\).

This then makes \(\beta: **Top** \to **CHaus**\) a reflector, so that the adjunction is a reflection between \(**Top**\) and \(**CHaus**\). Consequently we have the bijection

\[ \hom_{**Top**}(X, I(C)) \cong \hom_{**CHaus**}(\beta(X), C) \implies \hom_{**Top**}(X, C) \cong \hom_{**CHaus**}(\beta(X), C). \]

since \(I(C)\) is technically no different than from \(C\). This bijection is natural in both \(X\) and \(C\).

Let \(**Ab**_{**TF**}\) represent the category of abelian groups with torsion free elements (for a lack of better notation). Then we have a natural inclusion functor \(I: **Ab**_{**TF**} \to **Ab**\). Now consider the functor \(F : **Ab** \to **Ab**_{**TF**}\), which we define as follows:

  • Objects. Let \(G\) be an abelian group. Then \(F(G) = G_{TF}\) where
\[ G_{TF} = \{g \in G \mid g^n \ne e \text{ for } n = 1, 2, 3, \dots\}. \]

That is, it sends \(G\) to its underlying abelian group of torsion-free elements. It's not hard to show this is an abelian group. * Morphisms. Suppose \(\phi: G \to H\) is a morphism between abelian groups. Then we set \(F(\phi) = \phi_{TF}\) where

\[ \phi_{TF}: G_{TF} \to H_{TF} \qquad \phi_{TF}(g) = \phi(g). \]

Note that this definition will cause no issues, since \(\text{ord}(g) = \text{ord}(\phi(g))\). Thus we simply obtain \(\phi_{TF}\) by restricting \(\phi\) to \(G_{TF}\).

To show that \(F\) is left adjoint to \(I\), we need to demonstrate that there exists a universal morphism \(\eta_{G} : G \to I(F(G))\) for every \(G \in **Ab**\). Hence we propose \(\eta_{G}\) takes on the form

\[ \eta_{G}(g) = \begin{cases} g & \text{ if } \text{ord}(g) = \infty\\ e & \text{ otherwise. } \end{cases} \]

To show this is universal from \(G\) to \(I\), suppose we have a morphism \(\phi: G \to I(H)\), where \(H \in **Ab**_{**TF**}\). Then there exists a morphism \(\psi: F(G) \to H\) such that \(I(\phi) \circ \eta_{G} = \phi\). Visually, that is,

Sure such a morphism exists, but why the equality?

  • \(\bm{g \in \ker(\eta_G)}\). If \(g \in \ker(\eta_G)\), then \(g\) has finite order. Hence we see that \(\phi(g) = e\); this is because \(\text{ord}(\phi(g)) = \text{ord}(g) < \infty\), but the only element in \(I(H)\) with finite order is \(e\). We then have that \(g \in \ker(\phi)\). Therefore,
\[ I(\psi)\circ \eta_G(g) = I(\psi)(e) = e = \phi(g). \]

Hence \(I(\psi) \circ \eta_G = \phi\) if \(g \in \ker(\eta_{G})\). * \(\bm{g \not\in \ker(\eta_G)}\). if \(g \not\in \ker(\eta_G)\), then we know that \(\text{ord}(g) = \infty\). Therefore, we see that

\[ I(\psi) \circ \eta_G(g) = I(\phi)(g) = \phi(g). \]

Hence \(I(\psi) \circ \eta_G = \phi\) for \(g \not\in \ker(\eta_G)\).

By our previous work, we then have that \(I(\psi) \circ \eta_G = \phi\), as desired. Now \(\psi\) is of course unique based on its construction, since its definition depends directly on \(\phi\). We then have that \(\eta_G: G \to I(F(G))\) is universal from \(G\) to \(I\) for each \(G \in **Ab**\)!

We then have by Theorem 4.1 that \(F, I\) form an adjunction, so that \(F\) is the left adjoint of \(I\). Hence by definition, we see that \(**AB**_{**TF**}\) forms a full reflective subcategory of \(**Ab**\).

{\large Exercises \vspace{0.5cm}}

  • *1. Is FinSet a reflective subcategory of Set*?
  • *2.* Let \(G\) and \(H\) be a groups. Prove that
\[ G*H/[G*H, G*H] \cong G/[G,G]\oplus H/[H,H] \]

where \(G*H\) denotes the \hyperref[example:free_product]{\textcolor{blue}{free product}} of \(G\) and \(H\). (What this is saying is that \(F: **Grp** \to **Ab**\), the abelianization functor, preserves coproducts. Eventually, this fact will immediately follow by our knowledge of the adjunction \adjunction{Grp}{F}{Ab.}{U})