8.1. Preadditive Categories

Consider two abelian groups \((G, +)\) and \((H, \cdot)\) of Ab. Recall from group theory that we can turn the set \(\hom(G, H)\) into an abelian group \((\hom(G, H), *)\) as follows. Given \(\phi, \psi: G \to H\), we can create another group homomorphism \(\phi * \psi: G \to H\) where

\[\begin{align*} (\phi * \psi)(g) = \phi(g) \cdot \psi(g). \end{align*}\]

Observe that this is in fact a group homomorphism: if \(g, g' \in G\), then

\[\begin{align*} (\phi * \psi)(g + g') &= \phi(g + g') \cdot \psi(g + g')\\ &=\phi(g) \cdot \phi(g') \cdot \psi(g) \cdot \psi(g')\\ &\textcolor{Red}{=} \phi(g) \cdot \psi(g) \cdot \phi(g') \cdot \psi(g')\\ &= (\phi * \psi)(g) \cdot (\phi *\psi)(g'). \end{align*}\]

In the third step we utilized the fact that \((H, \cdot)\) is abelian. Thus \((\hom(G, H), *)\) is not necessarily a group unless \(H\) is an abelian group. Therefore, this construction doesn't extend to Grp.

At this point, your category-theory-voice in your head is probably asking: \begin{center} \begin{minipage}{0.8\textwidth} \textcolor{NavyBlue}{If \(H\) is an abelian group, can we create a functor \(F_H: **Ab** \to **Ab**\) where \(G \mapsto \hom(G, H)\)?} \end{minipage} \end{center}The answer is yes; the functor is actually contravariant, for suppose we have a group homomorphism

\[ \phi: G \to G'. \]

Then define the function

\[ F_H(\phi): \hom(G', H) \to \hom(G, H) \]

where \begin{statement}{NavyBlue!10}

\[ F_H(\phi)(\psi: G' \to H) = \psi \circ \phi: G \to H. \]

\end{statement} To verify functoriality, we have to check that this function is actually a group homomorphism. Towards that goal, consider \(\psi, \sigma: G \to H\). Then observe that for any \(g \in G\),

\[\begin{align*} F_H(\phi)(\psi + \sigma)(g) &= \phi(\psi(g) + \sigma(g))\\ &= \phi(\psi(g)) + \phi(\sigma(g))\\ &= F_H(\phi)(\psi)(g) + F_H(\phi)(\psi)(g) \end{align*}\]

which verifies that \(F_H(\phi)\) is a group homomorphism. Therefore, we see that \(F_H: **Ab** \to **Ab**\) is in fact a functor.

Now your category-theory-voice should be asking: \begin{center} \begin{minipage}{0.8\textwidth} \textcolor{NavyBlue}{If \(G\) is an abelian group, can we also create a functor \(F^G: **Ab** \to **Ab**\) where \(H \mapsto \hom(G, H)\)?} \end{minipage} \end{center}One can easily show that the answer is yes. In this direction, the functor is covariant. That is, for \(\psi: H \to H'\), we have that

\[ F^G(\psi): \hom(G, H) \to \hom(G, H') \]

where \begin{statement}{NavyBlue!10}

\[ F^G(\psi)(\phi: G \to H) = \psi \circ \phi: G \to H'. \]

\end{statement} Note that for our functors, we have that

\[ F_H(G) = F^G(H). \]

This is bifunctor-ish. Therefore, our category theory voice is now asking: \begin{center} \begin{minipage}{0.8\textwidth} \textcolor{NavyBlue}{Do we have a bifunctor \(F: **Ab**\times **Ab** \to **Ab**\) on our hands, where \(F(G, H) = \hom(G, H)\)? } \end{minipage} \end{center}To see if this answer is true, we ought to be able to show that, given \(\phi: G' \to G\) and \(\psi: H \to H'\), the diagram

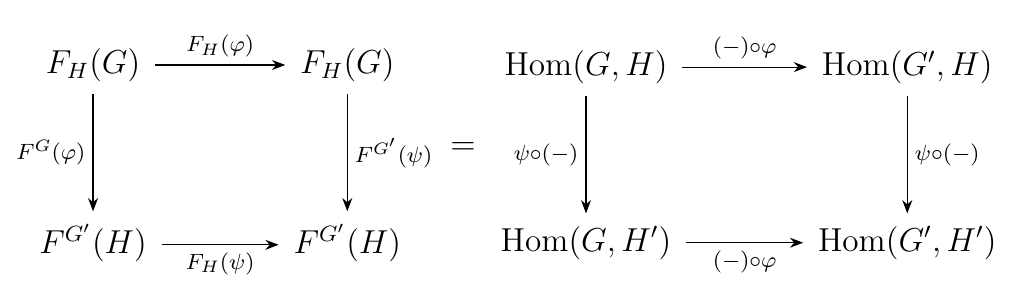
is commutative. The above diagram is in fact commutative since function composition is associative! That is, given \(\sigma: G \to H\), observe that going right and then down gives

\[\begin{align*} \psi \circ (\sigma \circ \phi) \end{align*}\]

while going down and then right gives

\[\begin{align*} (\psi \circ \sigma) \circ \phi. \end{align*}\]

Hence we have commutativity of the above diagram, and we therefore have a true bifunctor \(F: **Ab**\times**Ab** \to **Ab**\) where

\[ F(G,H) = \hom(G, H). \]

\textcolor{NavyBlue}{What this really shows is that \(\hom(-, -)\) is a functor; specifically, a bifunctor. So while we typically think of \(\hom(G, H)\) as a set, it had hidden functorial properties. Thus what makes Ab special is that plugging in abelian groups outputs an abelian group, and this is not the case with other constructions (e.g. Grp).}

Let us now consider a new observation of \(**Ab**\). For any triple of abelian groups

\[ (G, \star), (H, +), (K, \cdot) \]

we can create abelian groups

\[\begin{align*} &\big(\hom(G, H), +'\big) &&(\phi_1 +' \phi_2)(g) = \phi_1(g) + \phi_2(g) \\ &\big(\hom(H, K), \cdot'\big) &&(\psi_1 \cdot' \psi_2)(h) = \psi_1(h)\cdot \psi_2(h) \\ &\big(\hom(G, K), *\big) &&(\sigma_1 * \sigma_2)(g)= \sigma_1(g) \cdot \sigma_2(g) \\ \end{align*}\]

where \(\phi_i \in \hom(G, H), \psi_i \in \hom(H, K)\) and \(\sigma_i \in \hom(G, K)\) for \(i = 1, 2\). Now since these are abelian groups in Ab, there is a composition operator

\[ \circ: \hom(G, H)\times \hom(H,K) \to \hom(G, K) \]

where \(\circ(\phi: G \to H, \psi: H \to K ) \mapsto \psi \circ \phi: G \to K\). However, we now run into a problem where our operators might not play nicely with each other. Specifically, is it true that

\[ \psi \circ (\phi_1 +' \phi_2) = (\psi \circ \phi_1) * (\psi \circ \phi_2) \]

or

\[ (\psi_1 \cdot' \psi_2) \circ \phi = (\psi_1 \circ \phi) * (\psi_2 \circ \phi)? \]

For the first case, the answer is yes. Observe that

\[\begin{align*} \psi \circ (\phi_1 +' \phi_2)(g) &= \psi(\phi_1(g) + \phi_2(g))\\ &= \psi(\phi_1(g) + \phi_2(g))\\ &= \psi(\phi_1)(g) \cdot \psi(\phi_2)(g)\\ &= \big((\psi \circ \phi_1) * (\psi \circ \phi_2)\big)(g). \end{align*}\]

\textcolor{NavyBlue}{The reason we have linearity here is because of the way we defined the group operations on the homsets. The definition of these operations is intuitively correct, but we get accidentally get an extra bonus of obtaining linearity so that we don't have to worry about the above equations not holding.}

In order to mimic this behavior, we abstract this into a category to define a Ab-category.

An Ab-category or Preadditive Category is a category \(\mathcal{C}\) such that, for each pair of objects \(A, B\), there exists an abelian group operation \(+\) on the set \(\hom(A, B)\) such that

\[\begin{align*} &\circ: \hom(A, B)\times \hom(B, C) \to \hom(A, C)\\ &(f, g) \mapsto g \circ f \end{align*}\]

is bilinear. What we mean by bilinear is that, given morphisms \(f, g: A \to B\) and \(h, k: B \to C\), we have that \begin{statement}{Red!10}

\[\begin{align} (h + k) \circ f = h \circ f + k \circ f\\ h \circ (g + f) = h \circ g + h \circ f. \end{align}\]

\end{statement}

\textcolor{NavyBlue}{Note that since we demand that \(\hom_{\cc}(A, B)\) always be a group, we see that any category such that \(\hom_{\cc}(A, B) = \varnothing\) can never be an abelian group. A group always requires the existence of an identity; a demand that an empty set can never meet}. Therefore, as an example, any discrete category cannot be a preadditive category because all of the nontrivial homsets are empty.

As we demonstrated building up to this definition, Ab is a trivial example of a preadditive category. A less trivial example is \(**Vect**_K\) where \(K\) is a field, but this is nearly automatic since this takes advantage of the fact that vector spaces have their own hidden abelian group structure.

Suppose \(\cc\) is a one object category \(R\) which is also preadditive. Then this means that we have two binary operations \(+\) and \(\circ\) on the abelian group \(\hom_{\cc}(R, R)\) such that

\[\begin{align*} (h + k) \circ f = h \circ f + k \circ f\\ h \circ (g + f) = h \circ g + h \circ f. \end{align*}\]

However, this is simply a ring! The addition is the ring addition, while the ring multiplication is given by composition. Conversely, a ring regarded as the homset of a one object category can be defined to be an abelian category. This is because when regarding a group as a one object category, the group operation becomes the composition operation. Thus adding the extra axiom of an addition bilinear operation grants us that the category is preadditive.

Let \(\cc\) be a preadditive category. Then \(\cc\op\) is also a preadditive category. To demonstrate this, we know that every pair of objects \(A, B \in \cc\) gives rise to a group \((\hom_{\cc}(A, B), +)\) for some operation \(+\). This allows us to place a group structure \(+'\) on \(\hom_{\cc\op}(B, A)\) where for two \(f\op, g\op: B \to A\) in \(\cc\op\),

\[ f\op +' g\op = (f + g)\op. \]

That is, we rely on the preexisting group operation \(+\) from \(\hom_{\cc}(A, B)\). Given that the composition operator of \(\cc\op\) is \(\circ\op\), we can check that this satisfies the bilinearity conditions of \(\circ\op\). Suppose \(h\op, k\op : B \to A\) are two morphisms in \(\hom(B, A)\) which are composable with some \(f\op\). Then

\[\begin{align*} (h\op +' k\op)\circ\op f\op = (h + k)\op \circ \op f\op &= f \circ (h + k)\\ &= f \circ h + f \circ k \\ &= h\op \circ\op f\op +' k\op \circ\op f\op. \end{align*}\]

The other direction can be verified dually, so that the the group operation \(+'\) distributes bilinearly over \(\circ\op\). Therefore, \(\cc\op\) is a preadditive category.

If \(\cc\) is preadditive, then the functor category \(\cc^J\) is preadditive. To demonstrate this, consider the hom-set \(\hom_{\cc^J}(F, G)\) between two functors \(F, G: J \to \cc\). Now consider two natural transformations \(\eta, \epsilon \in \hom_{\cc^J}(F, G)\). Then for each \(f \in \hom_{\cc}(A, B)\), the familiar diagram commutes.

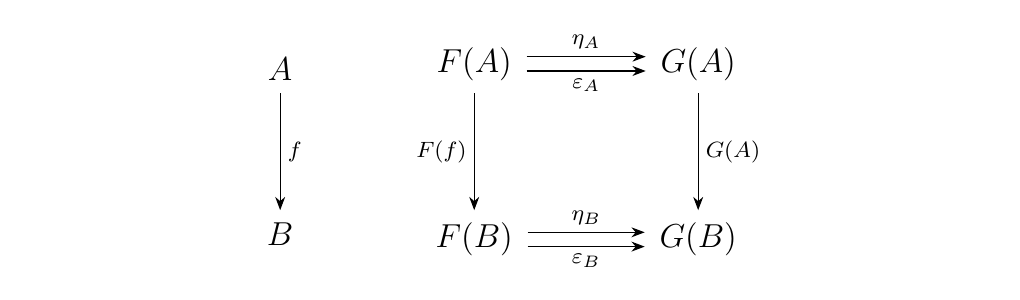This diagram tells us that \(G(f) \circ \eta_A = \eta_B \circ F(f)\) and that \(G(f) \circ \epsilon_A = \epsilon_B \circ F(f)\). However, since \(\cc\) is abelian, we can combine these morphisms and add both equations to get

\[ G(f) \circ \eta_A + G(f) \circ \epsilon_A = \eta_B \circ F(f) + \epsilon_B \circ F(f) \implies G(f) \circ (\eta_A + \epsilon_A) = (\eta_B + \epsilon_B) \circ F(f). \]

Hence the diagram below

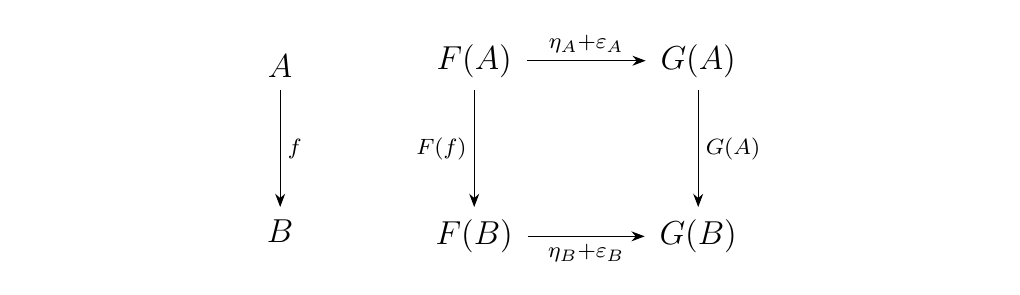commutes. Therefore, using the group product of \((\hom_{\cc}(F(A), F(B)), +)\), we've derived a new natural transformation from \(F\) to \(G\) using \(\eta\) and \(\epsilon\) in \(\hom_{\cc^J}(F, G)\). This allows us to endow the homset \(\hom_{\cc^J}(F, G)\) with the operation \(+'\) defined so that for two \(\eta, \epsilon \in \hom_{\cc^J}(F, G)\), \(\eta + ' \epsilon\) is the natural transformation where for each object \(A\)

\[ (\eta +' \epsilon)_A = \eta_A + \epsilon_A \]

where \(+\) is the group operation on \((\hom_{\cc}(F(A), G(A)), +)\). The fact that this distributes bilinearly over the composition operator is inherited from \(\cc\), and can easily be verified, so that \(\cc^J\) is preadditive.

Let \(\cc\) be a category such that for every pair of objects \(A, B\), the hom set \(\hom_{\cc}(A, B)\) is nonempty. Then we can create the category \(\text{PreAdd}(\cc)\) where the objects are the same as \(\cc\), except each \(\hom_{\text{PreAdd}(\cc)}(A, B)\) is now regarded as the free abelian group generated by the elements of \(\hom_{\cc}(A, B)\). This results in a preadditive category if we force the composition operator \(\circ'\) in \(\text{PreAdd}(\cc)\) to be bilinear. This forcing makes sense in our case since, if \(\sum_{f \in \hom_{\cc}(A,B)}n_f f, \sum_{f \in \hom_{\cc}(A,B)}n'_f f\) are two arbitrary elements in \(\hom_{\text{PreAdd}(\cc)}(A, B)\), then if \(\sum_{k \in \hom_{\cc}(B,C)}m_k k \in \hom_{\text{PreAdd}(\cc)}(B, C)\) for some object \(C\), where \(n_f, n'_f, m_k\) are all nonzero for finitely many integers, then

\[\begin{align*} &\sum_{k \in \hom_{\cc}(B,C)}m_k k \circ' \left( \sum_{f \in \hom_{\cc}(A,B)}n_f f + \sum_{f \in \hom_{\cc}(A,B)}n'_f f \right)\\ &= \sum_{f \in \hom_{\cc}(A,B)}\sum_{k \in \hom_{\cc}(B, C)}n_f \cdot m_k(k \circ f) + \sum_{f \in \hom_{\cc}(A,B)}\sum_{k \in \hom_{\cc}(B, C)}n'_f \cdot m_k(k\circ f) \end{align*}\]

and the above last expression is in fact an element of \(\hom_{\text{PreAdd}(\cc)}(A, C)\).