Skip to content

8.2. Additive Categories

Let \(G\) and \(H\) be abelian groups in Ab. A natural question to ask in any given category is if a binary product such at \(G \times H\) exists in the category. In our case, the answer is yes; it is the direct sum \(G \oplus H\). The direct sum satisfies the universal property

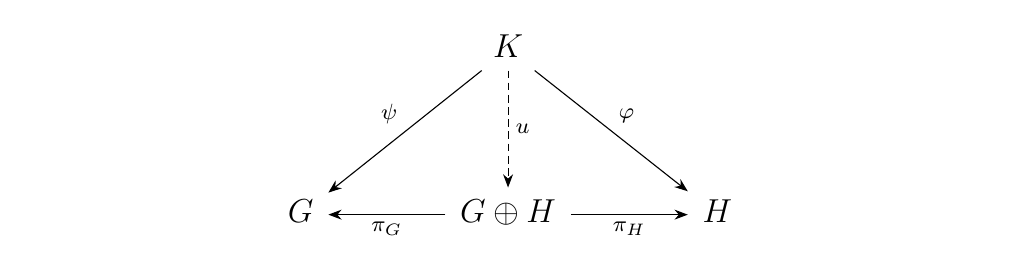Here, \(K\) is a third group, \(\phi\) and \(\psi\) are arbitrary group homomorphisms, and \(\pi_G, \pi_H\) are the natural projection morphisms. Interestingly, this object also satisfies the universal property

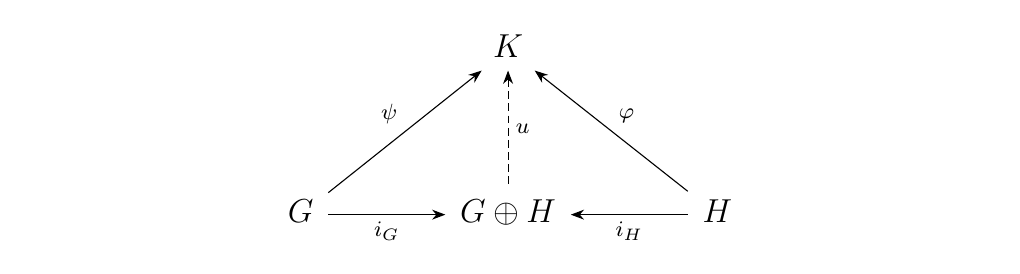Here \(i_G\) and \(i_H\) are the natural injections, e.g. \(i_G(g) = g \otimes e_H\). However, this implies that \(G \oplus H\) is a coproduct! What this implies is that \textcolor{NavyBlue}{product and coproducts coincide in Ab}. This is actually a pretty remarkable property because this isn't the case even in nice categories. For example, in Set, products and coproducts are definitely distinct.

\[\begin{center} Why is this the case? \end{center}\]

Let \(\cc\) be a preadditive category with a zero object \(z\). Then for any objects \(A, B \in \cc\), the following are equivalent

  • \((i)\) \(A \times B\) exists
  • \((ii)\) \(A \amalg B\) exists

Moreover, there exists an isomorphism

\[ \prod_{i \in \lambda} A_i \isomarrow \coprod_{i \in \lambda}A_i \]

for any objects \(A_i \in \cc\).

We only demonstrate one direction because the proof is self-dual.

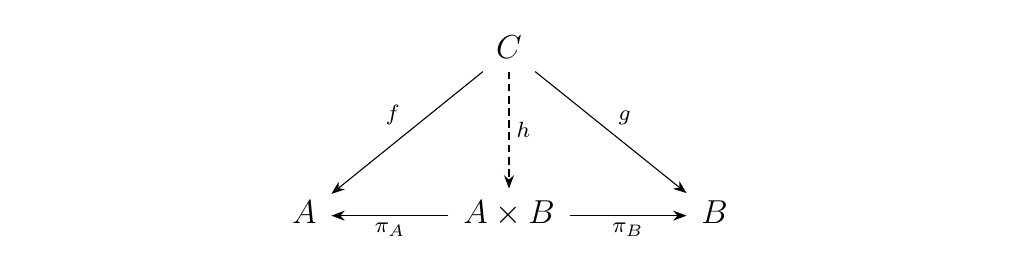
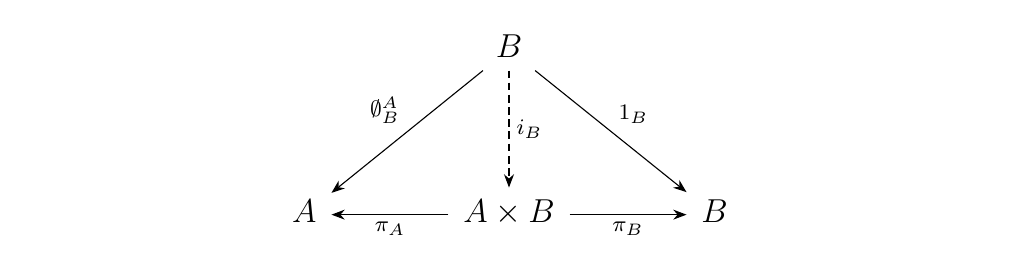
Suppose \(A \times B\) exists. Then then if \(C\) is an object equipped with morphisms \(f: C \to A\) and \(g: C \to B\), the following diagram must hold.

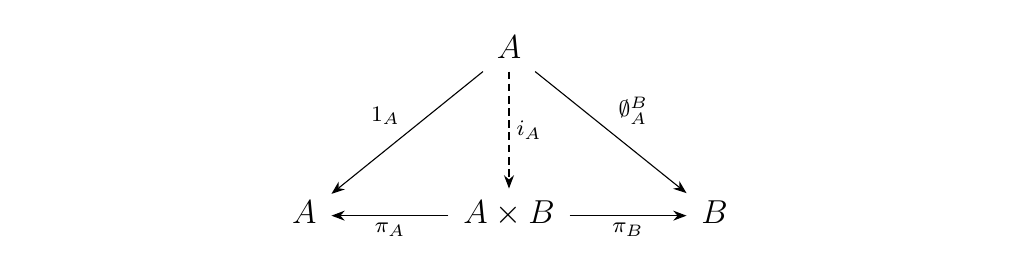
Equip \(A\) with the morphisms \(1_A: A \to A\) and the unique
zero morphism \(\emptyset_A^B: A \to B\). Then there exists a unique \(i_A: A \to A \times B\) such that the diagram commutes.

Symmetrically, equip \(B\) with the unique zero morphism \(\emptyset_B^A: B \to A\) and \(1_B: B \to B\). Then there exists a unique \(i_B: B \to A\times B\) such that the diagram commutes.

Now we'll demonstrate that we have a coproduct structure on our hands. To do this, suppose we have an object \(C\) equipped with morphisms \(f: A \to C\) and \(g: B \to C\). Then we can construct a morphism \(h\) such that the following diagram commutes.

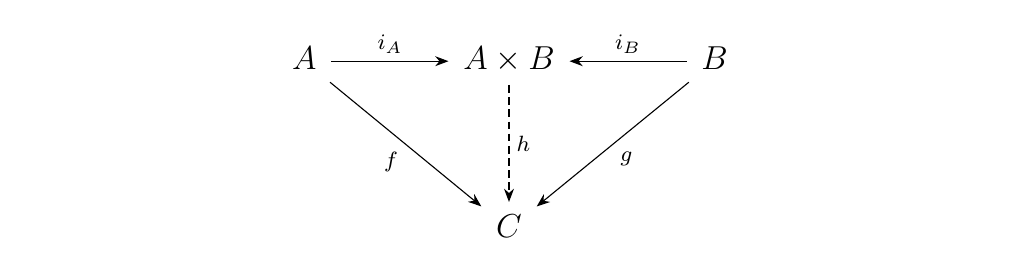Observe that \(h = f\circ \pi_A + g \circ \pi_B\) suffices, where \(+\) is the group operation on the abelian group \(\hom(A \times B, C)\). Observe that

\[\begin{align*} h \circ i_A &= (f\circ \pi_A + g \circ \pi_B) \circ i_A\\ &= f \circ (\pi_A \circ i_A) + g \circ (\pi_B \circ i_A)\\ &= f. \end{align*}\]

Similarly,

\[\begin{align*} h \circ i_B &= (f\circ \pi_A + g \circ \pi_B) \circ 1_B\\ &= f \circ (\pi_A \circ 1_B) + g \circ (\pi_B \circ 1_B)\\ &= g. \end{align*}\]

Hence the commutativity of the above diagram holds; therefore, we see that \(A \times B\) is also a coproduct. Finally, recall that if two distinct objects satisfy the same universal property, they are necessarily isomorphic; therefore the existence of an isomorphism between the product and coproduct is immediate. \textcolor{NavyBlue}{The above proof is not hard, but it's also not trivial. Moreover, there are three extremely important ingredients we utilized that demonstrate that the assumptions we've made so far are actually necessary and useful.}

  • This proof does not hold for a category without a zero object because there is not, in general, an obviously conceivable morphism to go from any two objects \(A\) and \(B\).
  • Notice that calculating \(h\) was only possible because we had an abelian group operation.
  • Finally, notice that we utilized bilinearity of the composition operator in order to calculate \(h \circ i_A\) and \(h \circ i_B\) and thereby verify the universal property.

Therefore, all of our assumptions so far have been necessary and useful. And all of this now motivates the following definition.

Let \(\cc\) be an abelian category. A biproduct of two objects \(A, B\) of \(\cc\) is an object \(A \otimes B\) which is both a product and coproduct. \ \textcolor{Purple}{Equivalently}, A biproduct is an object \(A \oplus B\) equipped with morphisms

\[\begin{align*} &\pi_A: A \oplus B \to A && i_A: A \to A \oplus B\\ &\pi_B: A \oplus B \to B && i_B: B \to A \oplus B \end{align*}\]

such that

  • 1. \(\pi_A \circ i_A = 1_A\)
  • 2. \(\pi_B \circ i_B = 1_B\)
  • 3. \(i_A \circ \pi_A + i_B \circ \pi_B = 1_{A\oplus B}\)

An Additive Category is a preadditive category \(\cc\) such that finite biproducts exist.

Consider the category \(**Grp**\).